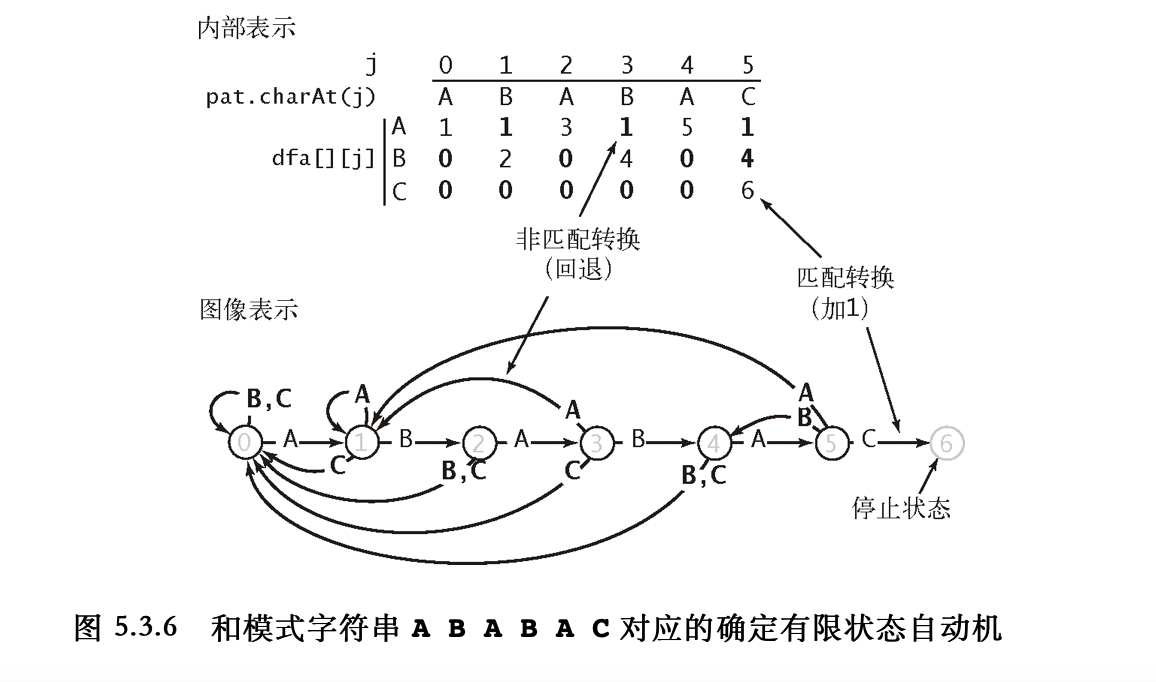
处理技巧

折半

加倍公式

rk‾(r−12)k‾=(2r)2k‾/22k,k⩾0\displaystyle r^{\underline{k}} \left(r - \frac{1}{2} \right) ^{\underline{k}} = (2r)^{\underline{2k}} / 2^{2k}, \quad k \geqslant 0

证明很简单，直接展开就可以，下面看几个推广

(1)\textbf{(1)}

(rk)(r−1/2k)=(2r2k)(2kk)/22k,k∈Z\displaystyle \binom{r}{k} \binom{r-1/2}{k} = \binom{2r}{2k} \binom{2k}{k} / 2^{2k}, \quad k \in \mathbb{Z}

证明方法，在加倍公式的两边同时除以 (k!)2(k!)^2

(2)\textbf{(2)}

(n−1/2n)=(2nn)/22n\displaystyle \binom{n - 1/2}{n} = \binom{2n}{n} / 2^{2n}

在 (1)\textbf{(1)} 中令 r=k=nr = k = n 即可

(3)\textbf{(3)}

(−1/2n)=(−14)n(2nn),n∈Z\displaystyle \binom{-1/2}{n} = \left(\frac{-1}{4} \right)^n \binom{2n}{n}, \quad n \in \mathbb{Z}

对 (2)\textbf{(2)} 反转上指标即可

(4)\textbf{(4)}

在 (1)\textbf{(1)} 中令 r=12n\displaystyle r = \frac{1}{2} n，可以得出

∑k(n2k)(2kk)2−2k=∑k(n/2k)((n−1)/2k)=(n−1/2⌊n/2⌋)\displaystyle \sum_k \binom{n}{2k} \binom{2k}{k} 2^{-2k} = \sum_k \binom{n/2}{k} \binom{(n-1)/2}{k} = \binom{n-1/2}{\left\lfloor n/2 \right\rfloor}

最后一步用了范德蒙卷积推广 (1)\textbf{(1)}

(5)\textbf{(5)}

∑k(2kk)(2n−2kn−k)=4n,n⩾0\displaystyle \sum_{k} \binom{2k}{k} \binom{2n-2k}{n-k} = 4^n, \quad n \geqslant 0

实际上，根据推广 (3)\textbf{(3)}，可以得到

(−1/2k)(−1/2n−k)=(−14)k(2kk)⋅(−14)n−k(2(n−k)n−k)\displaystyle \binom{-1/2}{k} \binom{-1/2}{n-k} = \left(\frac{-1}{4} \right)^{k} \binom{2k}{k} \cdot \left(\frac{-1}{4} \right)^{n-k} \binom{2(n-k)}{n-k}

=(−1)n4n(2kk)(2n−2kn−k)\displaystyle = \frac{(-1)^n}{4^n} \binom{2k}{k} \binom{2n-2k}{n-k}

根据范德蒙卷积

∑k(−1/2k)(−1/2n−k)=(−1n)=(−1)n\displaystyle\sum_{k} \binom{-1/2}{k} \binom{-1/2}{n-k} = \binom{-1}{n} = (-1)^n

在推广 (3)\textbf{(3)} 的结果基础上，两边同时对 kk 求和，即可证明

差分

差分用来计算 (nk)(−1)k\displaystyle \binom{n}{k}(-1)^k 的部分和

Δf(x)=f(x+1)−f(x)\Delta f(x) = f(x+1) - f(x)

一般来说，nn 阶差分是

Δnf(x)=∑k(nk)(−1)n−kf(x+k),n⩾0\Delta^n f(x) = \sum_{k} \binom{n}{k} (-1)^{n-k} f(x+k), \quad n \geqslant 0

证明如下，定义算子 Ef(x)=f(x+1)Ef(x) = f(x+1)，算子 Δ=E−1\Delta = E - 1

Δn=(E−1)n=∑k(nk)Ek(−1)n−k\displaystyle \Delta^n = (E-1)^n = \sum_k \binom{n}{k} E^k (-1)^{n-k}，EkE^k 即为 f(x+k)f(x+k)

对于负的下降幂

f(x)=(x−1)−1‾=1xf(x) = (x-1)^{\underline{-1}} = \frac{1}{x}

举几个例子，Δ2f(x)=(−1)(−2)(x−1)−3‾\displaystyle \Delta^2 f(x) = (-1)(-2) (x-1)^{\underline{-3}}

对于 nn 阶差分，有一般性公式

Δn((x−1)−1‾)=(−1)n‾(x−1)−n−1‾=(−1)nn!x(x+1)⋯(x+n)\displaystyle \Delta^n \left((x-1)^{\underline{-1}} \right) = (-1)^{\underline{n}} (x-1)^{\underline{-n-1}} = (-1)^n \frac{n!}{x(x+1)\cdots (x+n)}

根据差分展开式

∑k(nk)(−1)kx+k=(−1)nΔn(1x)=n!x(x+1)⋯(x+n)=x−1(x+nn)−1,x∉{0,−1,⋯ ,−n}\displaystyle \sum_{k} \binom{n}{k} \frac{(-1)^k}{x+k} = (-1)^n \Delta^n \left(\frac{1}{x} \right) = \frac{n!}{x(x+1)\cdots (x+n)} = x^{-1} \binom{x+n}{n}^{-1}, \quad x \notin \{0, -1, \cdots, -n\}

多项式差分

对于一般 dd 次多项式，f(x)=adxd+ad−1xd−1+⋯+a1x1+a0x0\displaystyle f(x) = a_d x^d + a_{d-1} x^{d-1} + \cdots + a_1x^1 + a_0 x^0

一般来说可以将其表示成为下降幂的和，x2=x2‾+x1‾x^{2} = x^{\underline{2}} + x^{\underline{1}}，从而有

f(x)=bdxd‾+bd−1xd−1‾+⋯+b1x1‾+b0x0‾\displaystyle f(x) = b_d x^{\underline{d} } + b_{d-1}x^{\underline{d-1}} + \cdots + b_1x^{\underline{1}} + b_0 x^{\underline{0}}

实际上，bd=ad,b0=a0b_d = a_d, b_0 = a_0，对于 0⩽k⩽d0 \leqslant k \leqslant d，令 ck=k!⋅bkc_k = k! \cdot b_k，那么有

f(x)=cd(xd)+cd−1(xd−1)+⋯+c1(x1)+c0(x0)\displaystyle f(x) = c_d \binom{x}{d} + c_{d-1} \binom{x}{d-1} + \cdots + c_1 \binom{x}{1} + c_0 \binom{x}{0}

根据加法公式，可以推出 Δ((xk))=(xk−1)\displaystyle \Delta \left(\binom{x}{k} \right) = \binom{x}{k-1}

牛顿级数的 nn 阶差分可以表示为

Δnf(x)=cd(xd−n)+cd−1(xd−1−n)+⋯+c1(x1−n)+c0(x−n)\displaystyle\Delta^n f(x) = c_d \binom{x}{d-n} + c_{d-1} \binom{x}{d-1-n} + \cdots + c_1 \binom{x}{1-n} + c_0 \binom{x}{-n}

对于 ck(xk−n)\displaystyle c_k \binom{x}{k - n}，令 x=0x = 0，只有 cnc_n 这一项

Δnf(0)={cnn⩽d0n>d\displaystyle \Delta^n f(0) = \begin{cases} c_n & n \leqslant d \\ 0 & n > d \end{cases}

f(x)f(x) 的牛顿级数为

f(x)=Δdf(0)(xd)+Δd−1f(0)(xd−1)+⋯+Δf(0)(x1)+f(0)(x0)\displaystyle f(x) = \Delta^d f(0) \binom{x}{d} + \Delta^{d-1} f(0) \binom{x}{d-1} + \cdots + \Delta f(0) \binom{x}{1} + f(0) \binom{x}{0}

实际上，对 x=0x = 0 应用 nn 阶差分的一般表达式，(−1)nΔnf(0)=(−1)ncn\displaystyle (-1)^n \Delta^n f(0) = (-1)^n c_n，可以推出

(−1)ncn=∑k(nk)(−1)k(f(k))\displaystyle (-1)^nc_n = \sum_{k} \binom{n}{k} (-1)^k \left(f(k) \right)

∑k(nk)(−1)k(c0(k0)+c1(k1)+c2(k2)+⋯ )=(−1)ncn,n⩾0\displaystyle \sum_k \binom{n}{k} (-1)^k \left(c_0 \binom{k}{0} + c_1 \binom{k}{1} + c_2 \binom{k}{2} + \cdots \right) = (-1)^nc_n, \quad n \geqslant 0

实际上，多项式 a0+a1x+a2x2+⋯anxn\displaystyle a_0 + a_1x + a_2 x^2 + \cdots a_nx^n 总可以写成牛顿级数 c0(x0)+c1(x1)+⋯+cn(xn)\displaystyle c_0 \binom{x}{0} + c_1 \binom{x}{1} + \cdots + c_n \binom{x}{n}
令 cn=n!anc_n = n!a_n，得到恒等式

∑k(nk)(−1)k(a0+a1k+⋯ankn)=(−1)nn!an\displaystyle \sum_k \binom{n}{k} (-1)^k \left(a_0 + a_1k + \cdots a_nk^n \right) = (-1)^n n!a_n

差分的应用

牛顿级数
一般牛顿级数，根据之前的分析，Δnf(0)=cn\displaystyle \Delta^n f(0) = c_n，可以得到恒等式

f(x)=f(0)(x0)+Δf(0)(x1)+Δ2f(0)(x2)+Δ3f(0)(x3)+⋯\displaystyle f(x) = f(0) \binom{x}{0} + \Delta f(0) \binom{x}{1} + \Delta^2 f(0) \binom{x}{2} + \Delta^3 f(0) \binom{x}{3} + \cdots

类似泰勒级数，f(x)=g(a+x)f(x) = g(a+x) 的牛顿级数可以写成

g(a+x)=g(a)0!x0‾+Δg(a)1!x1‾+Δ2g(a)2!x2‾+Δ3g(a)3!x3‾+⋯g(a+x) = \frac{g(a)}{0!} x^{\underline{0}} + \frac{\Delta g(a)}{1!} x^{\underline{1}} + \frac{\Delta^2 g(a)}{2!} x^{\underline{2}} + \frac{\Delta^3 g(a)}{3!} x^{\underline{3}} + \cdots

证明很简单，因为 f(x)=g(a+x)f(x) = g(a+x)，对于 n⩾0n \geqslant 0 有 Δnf(0)=Δng(a)\Delta^n f(0) = \Delta^n g(a)

举个例子，不妨设 g(x)=(1+z)xg(x) = (1+z)^x，如果 ∣z∣<1|z| < 1，那么 Δg(x)=(1+z)x+1−(1+z)x=z(1+z)x\displaystyle \Delta g(x) = (1+z)^{x+1} - (1+z)^x = z(1+z)^x
所以有 Δng(x)=zn(1+z)x\displaystyle \Delta^n g(x) = z^n (1+z)^x

g(a+x)=∑nΔng(a)(xn)=(1+z)a∑n(xn)zn\displaystyle g(a+x) = \sum_n \Delta^n g(a) \binom{x}{n} = (1+z)^a \sum_n \binom{x}{n} z^n

以上结果收敛于 (1+z)a+x(1+z)^{a+x}

斯特林阶乘推广
根据牛顿级数，令 ln⁡x!=∑nsn(xn)=s0(x0)+s1(x1)+s2(x2)+⋯\displaystyle \ln x! = \sum_n s_n \binom{x}{n} = s_0 \binom{x}{0} + s_1 \binom{x}{1} + s_2 \binom{x}{2} + \cdots

现在 Δ(ln⁡x!)=ln⁡(x+1)!−ln⁡x!=ln⁡(x+1)\Delta (\ln x!) = \ln (x+1)! - \ln x! = \ln (x+1)，记 f(x)=ln⁡(x+1)f(x) = \ln (x+1)，根据差分展开

sn=Δn(ln⁡x!)∣x=0\displaystyle s_n = \Delta^n (\ln x!) \big|_{x = 0}
 =Δn−1(ln⁡(x+1))∣x=0\displaystyle \quad \ = \Delta^{n-1} \left (\ln (x+1) \right) \big|_{x = 0}

 =∑k(n−1k)(−1)n−1−kf(0+k)=∑k(n−1k)(−1)n−1−kln⁡(k+1)\displaystyle \quad \ = \sum_k \binom{n-1}{k} (-1)^{n-1-k} f(0+k) = \sum_k \binom{n-1}{k} (-1)^{n-1-k} \ln (k+1)

由此可以代入，举个例子，s4=ln⁡4−3ln⁡3+3ln⁡2s_4 = \ln 4 - 3\ln 3 + 3 \ln 2

反演

反演公式

g(n)=∑k(nk)(−1)kf(k) ⟺ f(n)=∑k(nk)(−1)kg(k)g(n) = \sum_k \binom{n}{k} (-1)^k f(k) \ \Longleftrightarrow \ f(n) = \sum_k \binom{n}{k} (-1)^k g(k)

证明如下，实际上，我们需要求 ∑k(nk)(−1)kg(k)\displaystyle \sum_k \binom{n}{k} (-1)^k g(k)

而对 k⩾0k \geqslant 0，我们有 g(k)=∑j(kj)(−1)jf(j)\displaystyle g(k) = \sum_j \binom{k}{j} (-1)^j f(j)

∑k(nk)(−1)kg(k)=∑k(nk)(−1)k∑j(kj)(−1)jf(j)=∑jf(j)∑k(nk)(kj)(−1)k+j\displaystyle \sum_k \binom{n}{k} (-1)^k g(k) = \sum_k \binom{n}{k}(-1)^k \sum_j \binom{k}{j} (-1)^j f(j) = \sum_j f(j) \sum_k \binom{n}{k} \binom{k}{j} (-1)^{k+j}

=∑jf(j)∑k(nj)(n−jk−j)(−1)k+j=∑jf(j)(nj)∑k(−1)k(n−jk)\displaystyle \quad = \sum_j f(j) \sum_k \binom{n}{j} \binom{n-j}{k-j} (-1)^{k+j} = \sum_{j} f(j)\binom{n}{j} \sum_k (-1)^k \binom{n-j}{k}

最后一步是做了代换，令 k=k−jk = k-j

=∑jf(j)(nj)(1−1)n−j\displaystyle \quad = \sum_j f(j) \binom{n}{j} (1-1)^{n-j}，此时只有 n−j=0n - j = 0 时，∑j\displaystyle \sum_j 的项 ≠0\neq 0，此时 (1−1)n−j=1(1-1)^{n-j} = 1

=∑jf(j)(nj)[n=j]=f(n)\displaystyle \quad = \sum_j f(j) \binom{n}{j} [n = j] = f(n)

重排问题

nn 个球迷抛帽子，有多少种方式 h(n,k)h(n, k) 使得恰好有 kk 个球迷得到他们自己的帽子
实际上，我们需要任选 kk 顶帽子，让其回到原来拥有者的手上，剩下的 n−kn-k 顶帽子，均不回到其拥有者手上

h(n,k)=(nk)h(n−k,0)=(nk)(n−k)D\displaystyle h(n, k) = \binom{n}{k} h(n-k, 0) = \binom{n}{k} (n-k)_D

nDn_D 表示 nn 个物品排列时移动了每一项，这个排列就是重排

研究 nDn_D，可以发现一个递推关系

n!=∑kh(n,k)=∑k(nk)(n−k)D=∑k(nk)kD,n⩾0\displaystyle n! = \sum_k h(n, k) = \sum_k \binom{n}{k} (n-k)_D = \sum_k \binom{n}{k} k_D, \quad n \geqslant 0

最后一步推导同样用了 n−k=kn - k = k 代换和二项式对称性

用反演公式，发现 g(n)=n!,f(k)=(−1)k⋅kDg(n) = n!, \quad f(k) = (-1)^k \cdot k_D，从而 g(k)=k!, f(n)=(−1)nnD\displaystyle g(k) = k!, \ f(n) = (-1)^n n_D

其解为 nD=(−1)n∑k(nk)(−1)kk!\displaystyle n_D = (-1)^n \sum_k \binom{n}{k} (-1)^k k!

考虑化简，将二项式阶乘展开

nD=∑0⩽k⩽nn!(n−k)!(−1)n+k=n!∑0⩽k⩽n(−1)kk!\displaystyle n_D = \sum_{0 \leqslant k \leqslant n} \frac{n!}{(n-k)!} (-1)^{n+k} = n! \sum_{0 \leqslant k \leqslant n} \frac{(-1)^k}{k!}

最后一步同样是做等价替换，令 k←n−kk \leftarrow n-k

对于 nDn_D 中的和式，不难发现它就是 ex∣x=−1\text{e}^x \Big|_{x = -1} 展开，实际上 e−1=∑k⩾0(−1)kk!\displaystyle \text{e}^{-1} = \sum_{k \geqslant 0} \frac{(-1)^k}{k!}

实际上，nD=n!e−O(k)n_D = \displaystyle \frac{n!}{e} - O(k)，做阶的估计需要排除的项为

O(k)=n!∑k⩾n+1(−1)kk!\displaystyle O(k) = n! \sum_{k \geqslant n+1} \frac{(-1)^k}{k!}，令 k′=k−n−1k' = k-n-1，之后所有的 kk 用 k′+n+1k'+n+1 代换

O(k)=n!∑k⩾0(−1)(k+n+1)(k+n+1)!=(−1)n+1n+1∑k⩾0(−1)k(n+1)!(k+n+1)!\displaystyle O(k) = n! \sum_{k \geqslant 0} \frac{(-1)^{(k+n+1)}}{(k+n+1)!} = \frac{(-1)^{n+1}}{n+1} \sum_{k \geqslant 0} (-1)^k \frac{(n+1)!}{(k+n+1)!}

 =(−1)n+1n+1(1−1n+2+1(n+2)(n+3)+⋯ )\displaystyle \quad \quad \ = \frac{(-1)^{n+1}}{n+1} \left(1 - \frac{1}{n+2} + \frac{1}{(n+2)(n+3)} + \cdots \right)

注意到 1−1n+2=n+1n+2\displaystyle 1 - \frac{1}{n+2} = \frac{n+1}{n+2}，O(k)∈(1n+2,1n+1)\displaystyle O(k) \in \left(\frac{1}{n+2}, \frac{1}{n+1} \right)

但是 nD∈Zn_D \in \mathbb{Z}，所以实际上等于 n!e\displaystyle \frac{n!}{e} 四舍五入到最近的整数

nD=⌊n!e+12⌋+[n=0]\displaystyle n_D = \left\lfloor \frac{n!}{e} + \frac{1}{2} \right\rfloor + [n = 0]

重排问题的生成函数

n!=∑k(nk)(n−k)D\displaystyle n! = \sum_k \binom{n}{k} (n-k)_D，两边同时除以 n!n!

1=∑k=0n1k!(n−k)D(n−k)!\displaystyle 1 = \sum_{k=0}^n \frac{1}{k!} \frac{(n-k)_D}{(n-k)!}，看成是多项式卷积

[xn]1=[xn](∑k=0n1k!xk⋅(n−k)D(n−k)!xn−k)\displaystyle [x^n] 1 = [x^n] \left(\sum_{k=0}^n \frac{1}{k!}x^k \cdot \frac{(n-k)_D}{(n-k)!} x^{n-k} \right)

注意到 <10!,11!,12!,⋯ >\displaystyle \left<\frac{1}{0!}, \frac{1}{1!}, \frac{1}{2!}, \cdots \right> 对应的生成函数为 ex\text{e}^x，不妨设 D(x)=∑k⩾0kDk!xkD(x) = \displaystyle \sum_{k \geqslant 0}\frac{k_D}{k!} x^k

那么可以写成卷积形式 11−x=exD(x)\displaystyle \frac{1}{1-x} = e^x D(x)

最后 D(x)=11−xe−x=11−x(10!x0−11!x1+12!x2−⋯ )D(x) = \displaystyle \frac{1}{1-x} e^{-x} = \frac{1}{1-x} \left(\frac{1}{0!}x^0 - \frac{1}{1!}x^1 + \frac{1}{2!}x^2 - \cdots \right)

根据 D(x)=∑k⩾0kDk!xk\displaystyle D(x) = \sum_{k \geqslant 0} \frac{k_D}{k!} x^k，取 [xn][x^n] 的项，有

[xn]D(x)=[xn](1+x+x2+⋯ )(10!x0−11!x+12!x2−⋯ )\displaystyle [x^n]D(x) = [x^n](1+x+x^2 + \cdots) \left(\frac{1}{0!}x^0 - \frac{1}{1!}x + \frac{1}{2!}x^2 - \cdots \right)

所以有 nDn!=∑k=0n(−1)kk!\displaystyle \frac{n_D}{n!} = \sum_{k = 0}^{n} \frac{(-1)^k}{k!}，这里是因为 11−x\displaystyle \frac{1}{1-x} 展开 xjx^j 的系数总是 11

重排问题的另一种递推

首先不难发现 h(n,n−2)h(n, n-2) 的值符合三角形数 {1,3,6,10,15,⋯ }\{1, 3, 6, 10, 15, \cdots \}，这很好证明

h(n,n−2)=(nn−2)2D=(n2)\displaystyle h(n, n-2) = \binom{n}{n-2} 2_D = \binom{n}{2}

再来看 h(n,0)−h(n,1)h(n, 0) - h(n, 1)

h(n,0)−h(n,1)=nD−n(n−1)D=(n!∑0⩽k⩽n(−1)kk!)−(n(n−1)!∑0⩽k⩽n−1(−1)kk!)\displaystyle h(n, 0) - h(n, 1) = n_D - n(n-1)_D = \left(n!\sum_{0 \leqslant k \leqslant n} \frac{(-1)^k}{k!} \right) - \left(n(n-1)! \sum_{0 \leqslant k \leqslant n-1} \frac{(-1)^k}{k!} \right)

 =n!(−1)nn!=(−1)n\displaystyle \quad \quad \ = n! \frac{(-1)^n}{n!} = (-1)^n

综上所述
nD=n(n−1)D+(−1)n\displaystyle n_D = n(n-1)_D + (-1)^n

特殊反演

拉格朗日反演

多项式 F(x)F(x) 和 G(x)G(x)常数项都为 00 且一次项不为 00，并且 F(G(x))=xF(G(x)) = x，此时称 F,GF, G 互为复合逆
同时也一定有 G(F(x))=xG(F(x)) = x

[xn]F(x)=1n[x−1](1G(x))n=1n[xn−1](xG(x))n[x^n]F(x) = \frac{1}{n}[x^{-1}] \left(\frac{1}{G(x)} \right)^n = \frac{1}{n} [x^{n-1}] \left(\frac{x}{G(x)} \right)^n

证明如下，记 F(x)F(x) 中 xkx^k 的项系数为 F[k]F[k]，因为 F(G(x))=xF(G(x)) = x

∑kF[k]⋅Gk(x)=x\displaystyle \sum_k F[k] \cdot G^k (x) = x，两边对 xx 微分

∑kF[k]⋅k⋅Gk−1(x)⋅G′(x)=1\displaystyle \sum_k F[k]\cdot k \cdot G^{k-1}(x) \cdot G'(x) = 1，然后两边同时除以 Gn(x)G^{n}(x)

∑kF[k]⋅k⋅Gk−n−1(x)⋅G′(x)=1Gn(x)\displaystyle \sum_k F[k] \cdot k \cdot G^{k-n-1}(x) \cdot G'(x) = \frac{1}{G^n(x)}，考虑 [x−1][x^{-1}] 的项

[x−1]∑kF[k]⋅k⋅Gk−n−1(x)⋅G′(x)=[x−1]1Gn(x)\displaystyle [x^{-1}]\sum_k F[k] \cdot k \cdot G^{k-n-1}(x) \cdot G'(x) = [x^{-1}]\frac{1}{G^n(x)}

对于 k≠nk \neq n，此时 Gk−n−1(x)G′(x)=1k−n(Gk−n(x))′\displaystyle G^{k-n-1}(x) G'(x) = \frac{1}{k-n} \left (G^{k-n}(x) \right)'

因为 G(x)G(x) 中没有常数项并且一次项不为 00，自然 (Gk−n(x))′, k≠n\left(G^{k - n}(x) \right)', \ k \neq n 时不会有 [x−1][x^{-1}] 的项，所以 [x−1][x^{-1}] 由 k=nk = n 贡献

[x−1]F[n]⋅n⋅G−1(x)G′(x)=[x−1]1Gn(x)\displaystyle [x^{-1}] F[n]\cdot n \cdot G^{-1}(x)G'(x) = [x^{-1}] \frac{1}{G^n (x)}

注意到 G′(x)G(x)=a1+a2x+a3x2+⋯a1x+a2x2+a3x3+⋯\displaystyle \frac{G'(x)}{G(x)} = \frac{a_1 + a_2x + a_3x^2 + \cdots }{a_1x + a_2x^2 + a_3x^3 + \cdots }

[x−1]G−1(x)G′(x)=1[x^{-1}] G^{-1}(x) G'(x) = 1，从而 F[n]⋅n=[x−1](1G(x))nF[n] \cdot n = [x^{-1}] \displaystyle \left(\frac{1}{G(x)} \right)^n，F[n]F[n] 就是 [xn]F(x)[x^n]F(x)

从而拉格朗日反演成立

另类拉格朗日反演

对于无法求逆的整式，可以考虑用分数域，转换为常系数非 00 的整式逆
比如 (−2x2+x)−1(-2x^2 + x)^{-1} 在 x=0x = 0 时不可求逆

若 F(x)F(x) 不可求逆，令 G(x)=F(x)xk\displaystyle G(x) = \frac{F(x)}{x^k}，使得 G(x)G(x) 有常数项，那么 1F(x)=x−k1G(x)\displaystyle \frac{1}{F(x)} = x^{-k} \frac{1}{G(x)}

以上面为例子，(−2x2+x)−1=(−2x+1)−1x−1=x−11−2x(-2x^2 + x)^{-1} = (-2x + 1)^{-1} x^{-1} = \displaystyle \frac{x^{-1}}{1-2x}

引理
对于常系数为 00 并且 [x1][x^1] 系数不为 00 的整式 F(x)F(x)，有

[x−1]F′(x)Fk(x)=[k=−1]\displaystyle [x^{-1}] F'(x)F^k(x) = [k = -1]

证明如下
当 k≠−1k \neq -1，有 F′(x)Fk(x)=(1k+1Fk+1(x))′\displaystyle F'(x)F^k(x) = \left(\frac{1}{k+1}F^{k+1}(x) \right)'，也是整式，没有 [x−1][x^{-1}] 项

当 k=−1k = -1，那么 [x−1]F′(x)F(x)=[x0]F′(x)F(x)/x\displaystyle [x^{-1}]\frac{F'(x)}{F(x)} = [x^0] \frac{F'(x)}{F(x)/x}

注意到 F(x)/xF(x)/x 可逆，F′(x)F(x)/x\displaystyle \frac{F'(x)}{F(x)/x} 的常数项实际上均为 F[1]F[1]，所以右边 =1= 1，引理证毕

拉格朗日反演的一般形式

nGk[n]=k⋅[x−k]F−n(x)\displaystyle nG^k[n] = k\cdot [x^{-k}] F^{-n}(x)，其中 Gk[n]G^k[n] 就是 [xn]Gk(x)[x^n] G^{k}(x)

证明如下
G(F(x))=x⟹Gk(F(x))=xk\displaystyle G(F(x)) = x \Longrightarrow G^{k}(F(x)) = x^k，两边同时对 xx 微分

((Gk)′(F))⋅F′=kxk−1\displaystyle \left((G^k)'(F) \right) \cdot F' = kx^{k-1}，展开并注意到，GkG^{k} 中第 ii 项对应为 Gk[i]⋅FiG^k[i] \cdot F^{i}

那么 (Gk)′\displaystyle (G^k)' 对应的第 ii 项为 (i⋅Gk[i])⋅Fi−1\left(i \cdot G^k[i]\right) \cdot F^{i-1}

∑i⩾0iGk[i]⋅Fi−1⋅F′=kxk−1\displaystyle \sum_{i \geqslant 0} iG^k[i] \cdot F^{i-1} \cdot F' = kx^{k-1}，两边同时乘上 F−nF^{-n}

∑i⩾0iGk[i]Fi−n−1F′=kxk−1⋅F−n\displaystyle \sum_{i \geqslant 0} iG^k[i] F^{i-n-1} F' = kx^{k-1} \cdot F^{-n}，考虑 [x−1][x^{-1}] 的项

[x−1]∑i⩾0iGk[i]Fi−n−1F′=[x−1]kxk−1⋅F−n\displaystyle [x^{-1}]\sum_{i \geqslant 0} iG^k[i] F^{i-n-1} F' = [x^{-1}]kx^{k-1} \cdot F^{-n}，根据引理

[x−1]Fi−n−1F′=[i−n−1=−1][x^{-1}]F^{i-n-1}F' = [i-n-1 = -1]，所以左边 ∑i⩾0iGk[i][i−n−1=−1]=[x−1]kxk−1F−n\displaystyle \sum_{i \geqslant 0} iG^k [i][i-n-1 = -1] = [x^{-1}] kx^{k-1} F^{-n}

等式右边，将 xk−1x^{k-1} 吸收进 [x−1][x^{-1}]，右边多项式还必须提供 xx 的幂指为 −1−(k−1)=−k-1-(k-1) = -k，即

nGk[n]=[x−k]kF−n\displaystyle nG^k[n] = [x^{-k}] kF^{-n}

nGk[n]=k⋅[x−k]F−n(x)\displaystyle nG^k[n] = k\cdot [x^{-k}] F^{-n}(x)

另类拉格朗日反演
当 k≠0k \neq 0 时，根据多项式微分对应关系，[xk]F(x)=1k[xk−1]F′(x)\displaystyle [x^k] F(x) = \frac{1}{k} [x^{k-1}]F'(x)

那么以上拉格朗日反演的结论，可以扩展为

nGk[n]=k[x−k]F−n(x)\displaystyle nG^k[n] = k[x^{-k}] F^{-n}(x)

nGk[n]=k⋅1−k[x−k−1]⋅(−n)F−n−1F′\displaystyle nG^k[n] = k \cdot \frac{1}{-k} [x^{-k-1}] \cdot (-n)F^{-n-1}F'

Gk[n]=[x−k−1]F−n−1F′\displaystyle G^k[n] = [x^{-k-1}] F^{-n-1}F'

扩展拉格朗日反演

G(F(x))=xG(F(x)) = x，F(x)F(x) 和 G(x)G(x) 常数项都为 00 并且一次项不为 00，HH 是另一个无要求的幂级数

[xn]H(G(x))=1n[x−1]H′(x)(1F(x))n\displaystyle [x^n]H(G(x)) = \frac{1}{n}[x^{-1}] H'(x)\left(\frac{1}{F(x)} \right)^n

证明如下，以下将 F(x)F(x) 简写为 FF
G(F)=x ⟹ H(G(F))=HG(F) = x \ \Longrightarrow \ H(G(F)) = H，这里令 T(x)=H(G(x))T(x) = H(G(x))，那么有
T(F)=HT(F) = H，展开后可以知道

∑iT[i]Fi=H\displaystyle \sum_i T[i]F^{i} = H，两边同时对 xx 微分

∑i⩾0iT[i]⋅Fi−1F′=H′\displaystyle \sum_{i \geqslant 0} i T[i] \cdot F^{i-1}F' = H'，然后两边同时乘以 F−nF^{-n}

∑iT[i]i⋅Fi−n−1F′=H′F−n\displaystyle \sum_i T[i]i \cdot F^{i-n-1}F' = H' F^{-n}，根据引理，取 [x−1][x^{-1}] 的项

∑iT[i]i[i−n−1=−1]=[x−1]H′F−n\displaystyle \sum_i T[i] i [i-n-1 = -1] = [x^{-1}] H'F^{-n}，从而有

T[n]=1n[x−1]H′F−n\displaystyle T[n] = \frac{1}{n} [x^{-1}] H'F^{-n}

有了拉格朗日反演基础，就可以处理一些广义二项级数问题了

相关练习
ZJOI2020 抽卡
EZEC-7 线段树
CF1349F2 Slime and Sequences (Hard Version)
参考解答
KrOI2021 Feux Follets 弱化版
大朋友和多叉树
参考解答
凸多边形正则划分问题
地底蔷薇

广义二项级数

广义二项级数定义如下

Bt(z)=∑n⩾0(tn+1n)zntn+1\mathcal{B}_t(z) = \sum_{n \geqslant 0} \binom{tn+1}{n} \frac{z^n}{tn+1}

或者等价写成 Bt(z)=∑n⩾0(tn)n−1‾znn!\displaystyle \mathcal{B}_t(z) = \sum_{n \geqslant 0} (tn)^{\underline{n-1}} \frac{z^n}{n!}

给出几个恒等式
(1)\textbf{(1)}
Bt(z)=zBt(z)t+1\displaystyle \mathcal{B}_t(z) = z\mathcal{B}_t(z)^t + 1，或者等价写成
Bt(z)1−t−Bt(z)−t=z\displaystyle \mathcal{B}_t(z)^{1-t} - \mathcal{B}_t(z)^{-t} = z

(2)\textbf{(2)}

Bt(z)r=∑n⩾0(tn+rn)rtn+rzn\displaystyle B_t(z)^r = \sum_{n \geqslant 0} \binom{tn+r}{n} \frac{r}{tn+r} z^n

(3)\textbf{(3)}

Bt(z)r1−t+tBt(z)−1=∑n⩾0(tn+rn)zn\displaystyle \frac{\mathcal{B}_t(z)^r}{1-t+t\mathcal{B}_t(z)^{-1}} = \sum_{n \geqslant 0} \binom{tn + r}{n} z^n

证明如下，对于 (1)\textbf{(1)}，令 F(z)=Bt(z)−1F(z) = \mathcal{B}_t(z) - 1，那么有
F(z)=z(1+F(z))t\displaystyle F(z) = z(1+F(z))^t

此时如果令 G(z)=z(1+z)tG(z) = \displaystyle \frac{z}{(1+z)^t}，那么 G(F(z))=zG(F(z)) = z，并且 G(z),F(z)G(z), F(z) 常数项为 00 并且一次项不为 00

根据拉格朗日反演，可以推知

[zn]F(z)=1n[zn−1](zG(z))n=1n(ntn−1)\displaystyle [z^n]F(z) = \frac{1}{n}[z^{n-1}] \left(\frac{z}{G(z)} \right)^n = \frac{1}{n} \binom{nt}{n-1}

利用吸收二项式，可以推出

1n(ntn−1)=11+nt(1+ntn)\displaystyle \frac{1}{n} \binom{nt}{n-1} = \frac{1}{1+nt} \binom{1+nt}{n}，于是我们得到

Bt(z)=∑n⩾0(1+ntn)11+ntzn\displaystyle \mathcal{B_t}(z) = \sum_{n \geqslant 0} \binom{1+nt}{n} \frac{1}{1+nt} z^n

接下来考虑证明 (2)\textbf{(2)}

之前在证明的过程中，令 Bt=F(z)+1\mathcal{B}_t = F(z) + 1，那么这里的推广，对于 Bt(z)r=(1+F(z))r\mathcal{B}_t(z)^r = (1+F(z))^r
那么构造 H(z)=(1+z)rH(z) = (1+z)^r，这样可以对 H(F(z))H(F(z)) 用扩展拉格朗日反演

[zn]Bt(z)r=[zn]H(F(z))=1n[zn−1]H′(z)(zG(z))n=rn[zn−1](1+z)nt+r−1\displaystyle [z^n]\mathcal{B}_t(z)^r = [z^n]H(F(z)) = \frac{1}{n} [z^{n-1}]H'(z) \left(\frac{z}{G(z)} \right)^n = \frac{r}{n} [z^{n-1}](1+z)^{nt+r-1}

于是我们有
[zn]Bt(z)r=rn(nt+r−1n−1)\displaystyle [z^n]\mathcal{B}_t(z)^r = \frac{r}{n} \binom{nt+r-1}{n-1}

利用吸收恒等式，rn(nt+r−1n−1)=rnt+r(nt+rn)\displaystyle \frac{r}{n} \binom{nt+r-1}{n-1} = \frac{r}{nt+r} \binom{nt+r}{n}，从而有

Bt(z)r=∑n⩾0(nt+rn)rnt+rzn\displaystyle \mathcal{B}_t(z)^r = \sum_{n \geqslant 0} \binom{nt+r}{n} \frac{r}{nt+r} z^n

接下来考虑证明 (3)\textbf{(3)}
同样根据 Bt(z)=1+F(z)\displaystyle \mathcal{B}_t(z) = 1 + F(z)，构造 H(z)=(1+z)r1−t+t(1+z)−1\displaystyle H(z) = \frac{(1+z)^r}{1-t+t(1+z)^{-1}}

这样的话，[zn]Bt(z)r1−t+tBt(z)−1=[zn]H(F(z))\displaystyle [z^n] \frac{\mathcal{B}_t(z)^r}{1-t+t\mathcal{B}_t(z)^{-1}} = [z^n]H(F(z))

根据拉格朗日反演
[zn]H(F(z))=1n[zn−1]H′(z)(zG(z))n\displaystyle [z^n]H(F(z)) = \frac{1}{n} [z^{n-1}] H'(z) \left(\frac{z}{G(z)} \right)^n

 =1n[zn−1](1+z)ntr(1+z)r−1(1−t+t(1+z)−1)+(1+z)rt(1+z)−2(1−t+t(1+z)−1)2\displaystyle \quad \quad \ = \frac{1}{n}[z^{n-1}] (1+z)^{nt} \frac{r(1+z)^{r-1}(1-t+t(1+z)^{-1}) + (1+z)^r t(1+z)^{-2}}{(1-t+t(1+z)^{-1})^2}

 =1n[zn−1](1+z)nt+r(r1−(t−1)z+t(1−(t−1)z)2)\displaystyle \quad \quad \ = \frac{1}{n}[z^{n-1}](1+z)^{nt+r} \left(\frac{r}{1-(t-1)z} + \frac{t}{(1-(t-1)z)^2} \right)

考虑将其展开，难点是第二项，实际上，第二项可以写成 (1−(t−1)z)−2(1-(t-1)z)^{-2}，用牛顿二项式展开求 n−i−1n-i-1 项
系数为 (−1)n−i−1(−2n−i−1)\displaystyle (-1)^{n-i-1} \binom{-2}{n-i-1}，然后反转上指标

 =1n∑i=0n−1(nt+ri)(r(t−1)n−1−i+t(n−i)(t−1)n−1−i)\displaystyle \quad \quad \ = \frac{1}{n} \sum_{i = 0}^{n-1} \binom{nt+r}{i} \left(r(t-1)^{n-1-i} + t(n-i)(t-1)^{n-1-i} \right)

 =1n((nt+r)∑i=0n−1(nt+ri)(t−1)n−1−i−t∑i=0n−1(nt+ri)i(t−1)n−1−i)\displaystyle \quad \quad \ = \frac{1}{n} \left((nt+r)\sum_{i = 0}^{n-1} \binom{nt+r}{i}(t-1)^{n-1-i} - t\sum_{i = 0}^{n-1} \binom{nt+r}{i} i(t-1)^{n-1-i} \right)

对第二个求和式，应用吸收恒等式

 =1n(nt+r)(∑i=0n−1(nt+ri)(t−1)n−1−i−t∑i=0n−1(nt+r−1i−1)⋅i(t−1)n−1−i)\displaystyle \quad \quad \ = \frac{1}{n}(nt+r) \left(\sum_{i = 0}^{n-1} \binom{nt+r}{i}(t-1)^{n-1-i} - t\sum_{i = 0}^{n-1} \binom{nt+r-1}{i-1} \cdot i(t-1)^{n-1-i} \right)

下面考虑对该式进行化简

 =1n(nt+r)[zn−1]((1+z)nt+r1−(t−1)z−tz(1+z)nt+r−11−(t−1)z)\displaystyle \quad \quad \ = \frac{1}{n}(nt+r) [z^{n-1}] \left(\frac{(1+z)^{nt+r}}{1-(t-1)z} - \frac{tz(1+z)^{nt+r-1}}{1-(t-1)z} \right)

 =1n[zn−1](nt+r)(1+z)nt+r−1(1+z−tz)1−(t−1)z=1n[zn−1](nt+r)(1+z)nt+r−1\displaystyle \quad \quad \ = \frac{1}{n}[z^{n-1}](nt+r) \frac{(1+z)^{nt+r-1}(1+z-tz)}{1-(t-1)z} = \frac{1}{n}[z^{n-1}] (nt+r)(1+z)^{nt+r-1}

最后得到 nt+rn(nt+r−1n−1)\displaystyle \frac{nt+r}{n} \binom{nt+r-1}{n-1}，证毕

广义指数级数

Et(z)=∑n⩾0(tn+1)n−1znn!\displaystyle \mathcal{E}_t(z) = \sum_{n \geqslant 0} (tn+1)^{n-1} \frac{z^n}{n!}

同样满足以下 33 个性质

(1)\textbf{(1)}
Et(z)−tln⁡Et(z)=z\displaystyle \mathcal{E}_t(z)^{-t} \ln \mathcal{E}_t(z) = z

(2)\textbf{(2)}
Et(z)r=∑n⩾0r(tn+r)n−1znn!\displaystyle \mathcal{E}_t(z)^r = \sum_{n \geqslant 0} r(tn+r)^{n-1} \frac{z^n}{n!}

(3)\textbf{(3)}
Et(z)r1−ztEt(z)t=∑n⩾0(tn+r)nznn!\displaystyle \frac{\mathcal{E}_t(z)^r}{1-zt\mathcal{E}_t(z)^t} = \sum_{n \geqslant 0} (tn + r)^n \frac{z^n}{n!}

证明如下
证明 (1)\textbf{(1)}，实际上如果令 F(z)=ln⁡Et(z)F(z) = \ln \mathcal{E}_t(z)，Et(z)=eF(z)\mathcal{E}_t(z) = \text{e}^{F(z)}

只要证明 F(z)etF(z)=z\displaystyle \frac{F(z)}{e^{tF(z)}} = z 是否成立即可，假设它成立，只要看看能否推出 Et(z)\mathcal{E}_t(z)
求一下 Et(z)\mathcal{E}_t(z) 是多少就可以了

考虑拉格朗日反演， Et(z)=eF(z)\mathcal{E}_t(z) = e^{F(z)}，令 H(z)=ezH(z) = e^z，Et(z)=eF(z)=H(F(z))\mathcal{E}_t(z) = e^{F(z)} = H(F(z))

根据之前条件，如果令 G(z)=zetz\displaystyle G(z) = \frac{z}{e^{tz}}，那么有 G(F(z))=zG(F(z)) = z，那么 G,FG, F 互为符合逆

用扩展拉格朗日反演

[zn]Et(z)=[zn]eF(z)=[zn]H(F(z))\displaystyle [z^n] \mathcal{E}_t(z) = [z^n] e^{F(z)} = [z^n]H(F(z))

=1n[zn−1]H′(z)(zG(z))n=1n[zn−1]ez(etz)n=(tn+1)n−1n!\displaystyle \quad \quad = \frac{1}{n} [z^{n-1}] H'(z) \left(\frac{z}{G(z)} \right)^n = \frac{1}{n}[z^{n-1}] e^z (e^{tz})^n = \frac{(tn+1)^{n-1}}{n!}

这恰好就是 Et(z)\mathcal{E}_t(z) 的定义表达式

接下来证明 (2)\textbf{(2)}，实际上就是求 erF(z)e^{rF(z)} 的 [xn][x^n] 项，那么很简单

[zn]erF(z)=1n[zn−1]rerz(etz)n=r(tn+r)n−1n!\displaystyle [z^n]e^{rF(z)} = \frac{1}{n} [z^{n-1}] re^{rz}(e^{tz})^n = r\frac{(tn + r)^{n-1}}{n!}

还有一种证明方法，是根据广义二项级数的极限表达式来证明

首先不难发现引理，lim⁡x→∞(xnk)x−k=nkk!\displaystyle \lim_{x \to \infty} \binom{xn}{k}x^{-k} = \frac{n^k}{k!}

直接展开就可以，lim⁡x→∞(xnk)x−k=lim⁡x→∞n(n−1x)(n−2x)⋯(n−n−k+1x)k!\displaystyle \lim_{x \to \infty} \binom{xn}{k} x^{-k} = \lim_{x \to \infty} \frac{n(n - \frac{1}{x})(n - \frac{2}{x}) \cdots (n - \frac{n-k+1}{x})}{k!}

那么根据引理，可以证明

lim⁡x→∞Bxt(zx)x=lim⁡x→∞∑n⩾0(nxt+xn)xxtn+x(zx)n\displaystyle \lim_{x \to \infty} \mathcal{B}_{xt} \left(\frac{z}{x} \right)^x = \lim_{x \to \infty}\sum_{n \geqslant 0} \binom{nxt+x}{n} \frac{x}{xtn + x} \left(\frac{z}{x}\right) ^n

=∑n⩾0lim⁡x→∞(x(nt+1)n)znxn(nt+1)=∑n⩾0(nt+1)n−1znn!=Et(z)\displaystyle \quad \quad = \sum_{n \geqslant 0} \lim_{x \to \infty} \binom{x(nt+1)}{n} \frac{z^n}{x^n(nt+1)} = \sum_{n \geqslant 0} (nt+1)^{n-1} \frac{z^n}{n!} = \mathcal{E}_t(z)

两边同时 rr 次幂，有 Et(z)r=lim⁡x→+∞Bxt(z/x)xr\displaystyle \mathcal{E}_t(z)^r = \lim_{x \to +\infty} \mathcal{B}_{xt} (z/x)^{xr}

接下来考虑证明 (3)\textbf{(3)}

在 (1), (2)\textbf{(1), (2)} 的证明中，已知以下结论
zEt(z)t=F(z),F(z)=ln⁡Et(z),Et(z)=eF(z)\displaystyle z\mathcal{E}_t(z)^t = F(z), \quad F(z) = \ln \mathcal{E}_t(z), \quad \mathcal{E}_t(z) = e^{F(z)}

[zn]erF(z)1−tF(z)=1n[zn−1](erz1−tz)′(etz)n\displaystyle [z^n] \frac{e^{rF(z)}}{1-tF(z)} = \frac{1}{n} [z^{n-1}] \left(\frac{e^{rz}}{1-tz} \right)' (e^{tz})^n

=1n[zn−1]e(nt+r)z(r1−tz+t(1−tz)2)\displaystyle \quad \quad = \frac{1}{n}[z^{n-1}] e^{(nt+r)z} \left(\frac{r}{1-tz} + \frac{t}{(1-tz)^2} \right)

=1n(∑i=0n−1(nt+r)ii!rtn−1−i+∑i=0n−1(nt+r)ii!t⋅(n−i)tn−1−i)\displaystyle \quad \quad = \frac{1}{n} \left(\sum_{i = 0}^{n-1} \frac{(nt+r)^i}{i!} rt^{n-1-i} + \sum_{i = 0}^{n-1} \frac{(nt+r)^i}{i!} t \cdot (n-i)t^{n-1-i}\right)

=1n∑i=0n−1(nt+r)ii!tn−1−i(nt+r−it)=1n(∑i=0n−1(nt+r)(nt+r)ii!tn−1−i−∑i=0n−1it⋅(nt+r)ii!tn−1−i)\displaystyle \quad \quad = \frac{1}{n} \sum_{i = 0}^{n-1} \frac{(nt+r)^i}{i!} t^{n-1-i} (nt+r-it) = \frac{1}{n} \left(\sum_{i = 0}^{n-1} (nt+r) \frac{(nt+r)^i}{i!} t^{n-1-i} - \sum_{i = 0}^{n-1} it \cdot \frac{(nt+r)^i}{i!} t^{n-1-i}\right)

括号里的部分，很显然是求 [xn−1][x^{n-1}] 这一项的系数
考虑第二部分的求和，可以写成

(nt+r)(nt+r)i−1(i−1)!⋅tn−i\displaystyle (nt+r) \frac{(nt+r)^{i-1}}{(i-1)!} \cdot t^{n-i}，如果写成卷积

∑i(nt+r)(nt+r)i−1(i−1)!\displaystyle \sum_{i} (nt+r) \frac{(nt+r)^{i-1}}{(i-1)!} 很像 (e(nt+r)z)′\left(e^{(nt+r)z} \right)'

实际上，∑i(nt+r)(nt+r)i−1(i−1)!\displaystyle \sum_{i} (nt+r) \frac{(nt+r)^{i-1}}{(i-1)!} 是 [zi−1](e(nt+r)z)′[z^{i-1}]\left(e^{(nt+r)z} \right)'，统一起来

将其写成 [zi]z⋅(e(nt+r)z)′\displaystyle [z^{i}] z \cdot \left(e^{(nt+r)z} \right)'，同样后面也可以写成 t⋅tn−i−1t \cdot t^{n-i-1}

这样，用卷积的形式来表示第二项求和式

[xn−1](z⋅(e(nt+r)z)′⋅t⋅11−tz)\displaystyle [x^{n-1}] \left(z\cdot (e^{(nt+r)z})' \cdot t \cdot \frac{1}{1-tz} \right)，这样可以将括号中的两种求和形式统一起来

=1n[zn−1]e(nt+r)z⋅(nt+r)(1−tz)1−tz=(nt+r)nn!\displaystyle \quad \quad = \frac{1}{n}[z^{n-1}] \frac{e^{(nt+r)z} \cdot (nt+r)(1-tz)}{1-tz} = \frac{(nt+r)^n}{n!}

证毕

简单应用

例 1

求 ∑i⩾012n+2i(n+2i)(n+2ii)\displaystyle \sum_{i \geqslant 0} \frac{1}{2^{n + 2i} (n + 2i)} \binom{n + 2i}{i}

这很显然可以转换成为广义二项级数的形式

1n2n∑i⩾0(2i+ni)n2i+n(14)i\displaystyle \frac{1}{n2^n} \sum_{i \geqslant 0} \binom{2i+n}{i} \frac{n}{2i + n} \left(\frac{1}{4} \right)^i

=1n2n∑i⩾0B2(14)n\displaystyle \quad = \frac{1}{n2^n} \sum_{i \geqslant 0} \mathcal{B}_2 \left(\frac{1}{4} \right)^n

下面的问题就是求 B2(z)\displaystyle \mathcal{B}_2(z)，有方程

B2(z)=zB2(z)2+1\displaystyle \mathcal{B}_2(z) = z\mathcal{B}_2(z)^2 + 1

求解得到 B2(z)=1−1−4z2z\displaystyle \mathcal{B}_2(z) = \frac{1- \sqrt{1-4z}}{2z}

实际上原式有两个根，而 lim⁡z→0(1+1−4z)/(2z)=∞\lim_{z \to 0} (1+\sqrt{1-4z})/(2z) = \infty，故这个根不符合条件，因为 z=0z = 0 时候多项式肯定不是 ∞\infty

带回去，就得到答案 1n\displaystyle \frac{1}{n}

例 2

bi=∑j⩾0aj(2i−ji−j)\displaystyle b_i = \sum_{j \geqslant 0} a_j \binom{2i-j}{i-j}，已知序列 <a>\left< a \right> 求 <b>\left< b \right>

这种很像二项级数的表达式，可以考虑转换成 OGF\text{OGF}，即生成函数

B(z)=∑i⩾0bizi\displaystyle B(z) = \sum_{i \geqslant 0} b_i z^i

 =∑i⩾0zi∑j⩾0aj(2i−ji−j)\displaystyle \quad \ = \sum_{i \geqslant 0} z^i \sum_{j \geqslant 0} a_j \binom{2i-j}{i-j}

 =∑j⩾0ajzj∑i⩾jzi−j(2i−ji−j)\displaystyle \quad \ = \sum_{j \geqslant 0} a_j z^j \sum_{i \geqslant j}z^{i-j} \binom{2i-j}{i - j}

 =∑j⩾0ajzj∑i⩾0zi(2i+ji)\displaystyle \quad \ = \sum_{j \geqslant 0}a_j z^j \sum_{i \geqslant 0} z^i \binom{2i+j}{i}

注意到 B2(z)j1−2+2B2(z)−1=∑i⩾0(2i+ji)zi\displaystyle \frac{\mathcal{B}_2(z)^j}{1-2+2\mathcal{B}_2(z)^{-1}} = \sum_{i \geqslant 0} \binom{2i+j}{i} z^i

从而 B(z)=12B2(z)−1−1∑j⩾0aj(zB2(z))j\displaystyle B(z) = \frac{1}{2 \mathcal{B}_2(z)^{-1} - 1} \sum_{j \geqslant 0} a_j \left(z \mathcal{B}_2(z) \right)^j

我们有 zB2(z)=1−1−4z2\displaystyle z\mathcal{B}_2(z) = \frac{1-\sqrt{1-4z}}{2}，令 u=1−4zu = \displaystyle \sqrt{1-4z}，就可以先算出和式

∑j⩾0aj⋅(1−u)j2j\displaystyle \sum_{j \geqslant 0} a_j \cdot \frac{(1-u)^j}{2^j}

然后考虑卷积即可，设卷积的结果是 ∑j⩾0cjuj\displaystyle \sum_{j \geqslant 0} c_j u^j

按根号幂级数展开卷积，并且在 O(nlog⁡n)O(n \log n) 计算即可

例 3
证明恒等式

B2(z)r1−4z=∑k(2k+rk)zk\displaystyle \frac{\mathcal{B}_2(z)^r}{\sqrt{1-4z}} = \sum_{k} \binom{2k+r}{k} z^k

该证明需要用到二叉树方程 F=x(1+F)2F = x(1+F)^2

这个方程来源是恒等式 (1)\textbf{(1)}，我们定义了
{F(x)=B2(x)−1F=x(1+F)2\displaystyle\begin{cases} F(x) = \mathcal{B}_2(x) - 1 \\ F = x(1+F)^2 \end{cases}

我们想要证明 11−4x(1−1−4x2x)m=∑n(2n+mn)xn\displaystyle \frac{1}{\sqrt{1-4x}} \left(\frac{1-\sqrt{1-4x}}{2x} \right)^m = \sum_n \binom{2n+m}{n}x^n

实际上，(1−1−4x2x)m=B2(x)=F(x)+1\displaystyle \left(\frac{1-\sqrt{1-4x}}{2x} \right)^m = \mathcal{B}_2(x) = F(x) + 1

由此只要证明

11−4⋅F(1+F)2⋅(1+F)m=(1+F)m+11−F\displaystyle \frac{1}{\sqrt{1- 4 \cdot \frac{F}{(1+F)^2}}} \cdot (1+F)^m = \frac{(1+F)^{m+1}}{1-F}

注意到 F(1+F)2=x\displaystyle \frac{F}{(1+F)^2} = x，令 G(x)=x(1+x)2\displaystyle G(x) = \frac{x}{(1+x)^2}，那么 G(F(x))=xG(F(x)) = x

可以考虑用拉格朗日反演

[xn](1+F)m+11−F=[xn]H(F(x))\displaystyle [x^n] \frac{(1+F)^{m+1}}{1-F} = [x^n] H(F(x))，其中 H(x)=(1+x)m+11−x\displaystyle H(x) = \frac{(1+x)^{m+1}}{1-x}

[xn](1+F)m+11−F=1n[xn−1]((1+x)m+11−x)′(1+x)2n\displaystyle [x^n] \frac{(1+F)^{m+1}}{1-F} = \frac{1}{n} [x^{n-1}] \left(\frac{(1+x)^{m+1}}{1-x} \right)' (1+x)^{2n}

=1n[xn−1](1+x)m+2n(2+m(1−x))(1−x)2\displaystyle \quad \quad = \frac{1}{n} [x^{n-1}] \frac{(1+x)^{m+2n} (2+m(1-x))}{(1-x)^2}

=1n[xn−1](m(1+x)m+2n1−x+2(1+x)m+2n(1−x)2)\displaystyle \quad \quad = \frac{1}{n} [x^{n-1}] \left(\frac{m(1+x)^{m+2n}}{1-x} + \frac{2(1+x)^{m+2n}}{(1-x)^2}\right)

=1n∑k⩽n−1(m(m+2nk)+2(m+2nk)(n−k))=1n∑k⩽n−1(m+2nk)(m+2n−2k)\displaystyle \quad \quad = \frac{1}{n} \sum_{k \leqslant n-1} \left(m \binom{m+2n}{k} + 2\binom{m+2n}{k}(n-k) \right) = \frac{1}{n} \sum_{k \leqslant n-1} \binom{m+2n}{k} (m+2n - 2k)

下面考虑将求和式写成卷积的形式

1n∑k(m+2nk)(m+2n)−(m+2nk)⋅2k\displaystyle \frac{1}{n}\sum_k \binom{m+2n}{k}(m+2n) - \binom{m+2n}{k} \cdot 2k

第一部分可以写成 [xn−1](m+2n)⋅(1+x)m+2n11−x[x^{n-1}] \displaystyle (m+2n)\cdot (1+x)^{m+2n} \frac{1}{1-x}

第二部分，多乘了一个 kk，不难想到应该是 (1+x)m+2n\displaystyle (1+x)^{m+2n} 提供幂指 [xk][x^k]，然后再乘以 kk，这像什么？

就是微分！如果构造 2⋅[xk]((1+x)m+2n)′⋅x2\cdot [x^k]\left( (1+x)^{m+2n} \right)' \cdot x，这样 [xk][x^k] 项系数约等于构成了第二部分

我们要 [xn−1][x^{n-1}] 怎么办？乘上一个 11−x\displaystyle \frac{1}{1-x} 就可以了

=1n[xn−1]((m+2n)(1+x)m+2n11−x−2((1+x)m+2n)′⋅x1−x)\displaystyle \quad \quad = \frac{1}{n} [x^{n-1}] \left((m+2n)(1+x)^{m+2n} \frac{1}{1-x} - \frac{2 \left((1+x)^{m+2n} \right)'\cdot x}{1-x} \right)

=1n[xn−1](m+2n)(1+x)m+2n−1\displaystyle \quad \quad = \frac{1}{n} [x^{n-1}] (m+2n) (1+x)^{m+2n-1}

=1n(m+2n−1n−1)(m+2n)=(m+2nn)\displaystyle \quad \quad = \frac{1}{n} \binom{m+2n-1}{n-1} (m+2n) = \binom{m+2n}{n}

例 4

证明 B−1(z)=1+1+4z2\displaystyle \mathcal{B}_{-1}(z) = \frac{1+\sqrt{1+4z}}{2}

根据广义二项式系数恒等式，我们有

B−1(z)2=z+B−1(z)\displaystyle \mathcal{B}_{-1}(z)^2 = z + \mathcal{B}_{-1}(z)，同样化为二次方程 B2−B−z=0B^2 - B - z = 0

求出 B−1(z)=1+1+4z2\displaystyle \mathcal{B}_{-1}(z) = \frac{1+ \sqrt{1+4z}}{2}，因为这样恰好满足 lim⁡z→0B−1(z)=1\lim_{z \to 0} \mathcal{B}_{-1}(z) = 1，另一个根舍掉

基于以上推论，不难发现两个恒等式

{B−1(z)=1+zB2(−z)B−1(z)=B2(−z)−1\displaystyle \begin{cases} \mathcal{B}_{-1}(z) = 1 + z\mathcal{B}_{2}(-z) \\ \mathcal{B}_{-1}(z) = \mathcal{B}_2(-z)^{-1}\end{cases}

基于此，根据例 3 的证明结果，不难推出

(1)\textbf{(1)}

B−1(z)r+11+4z=∑k(r−kk)zk\displaystyle \frac{\mathcal{B}_{-1}(z)^{r+1}}{\sqrt{1+4z}} = \sum_{k} \binom{r-k}{k}z^k

证明如下，因为 B2(−z)r=B−1(z)−r\displaystyle \mathcal{B}_2(-z)^{r} = \mathcal{B}_{-1}(z)^{-r}

代入例3的结果，令 z←−zz \leftarrow -z

B−1(z)−r1+4z=∑k(2k+rk)(−1)kzk\displaystyle \frac{\mathcal{B}_{-1}(z)^{-r}}{\sqrt{1+4z}} = \sum_{k} \binom{2k+r}{k} (-1)^{k} z^k

反转上指标，可以推出

=∑k(−k−r−1k)zk\displaystyle \quad \quad = \sum_{k} \binom{-k-r-1}{k}z^k，令 r←−r−1r \leftarrow -r-1

有 B−1(z)r+11+4z=∑k(r−kk)zk\displaystyle \frac{\mathcal{B}_{-1}(z)^{r+1}}{\sqrt{1+4z}} = \sum_k \binom{r-k}{k} z^k

另外，关于 B−1(z)\displaystyle \mathcal{B}_{-1}(z) 和 B2(−z)\mathcal{B}_2(-z) 之间还有其他联系

(2)\textbf{(2)}

B−1(z)n+1−(−z)n+1B2(−z)n+11+4z=∑k⩽n(n−kk)zk\displaystyle \frac{\mathcal{B}_{-1}(z)^{n+1} - (-z)^{n+1} \mathcal{B}_2(-z)^{n+1}}{\sqrt{1+4z}} = \sum_{k \leqslant n} \binom{n-k}{k} z^k

证明如下

考虑 k⩾nk \geqslant n 时 (−z)n+1B2(−z)n+11+4z\displaystyle \frac{(-z)^{n+1} \mathcal{B}_2(-z)^{n+1}}{\sqrt{1+4z}} 的 [zk][z^k] 系数

根据例3的结论，令 z←−zz \leftarrow -z

[zk](−z)n+1B2(−z)n+11+4z=(−1)n+1[zk−n−1]B2(−z)n+11+4z\displaystyle [z^k] \frac{(-z)^{n+1} \mathcal{B}_2(-z)^{n+1}}{\sqrt{1+4z}} = (-1)^{n+1} [z^{k-n-1}] \frac{\mathcal{B}_2(-z)^{n+1}}{\sqrt{1+4z}}

然后再一次做变量替换，z←−zz \leftarrow -z

=(−1)n+1(−1)k−n−1[zk−n−1]B2(z)n+11−4z\displaystyle \quad \quad = (-1)^{n+1}(-1)^{k-n-1} [z^{k-n-1}] \frac{\mathcal{B}_2(z)^{n+1}}{\sqrt{1-4z}}

根据例3的表达式展开

=(−1)k(2(k−n−1)+n+1k−n−1)=(−1)k(2k−n−1k)=(n−kk)\displaystyle \quad \quad = (-1)^k \binom{2(k-n-1) + n+1}{k-n-1} = (-1)^k \binom{2k-n-1}{k} = \binom{n-k}{k}

而 (n−kk)=[zk]B−1(z)n+11+4z\displaystyle \binom{n-k}{k} = [z^k] \frac{\mathcal{B}_{-1}(z)^{n+1}}{\sqrt{1+4z}}

右边减去左边，就得到了结果

那么根据 (2)\textbf{(2)}，可以得到封闭形式

∑k⩽n(n−kk)zk=11+4z((1+1+4z2)n+1−(1−1+4z2)n+1),n⩾0\displaystyle \sum_{k \leqslant n} \binom{n-k}{k} z^k = \frac{1}{\sqrt{1+4z}}\left( \left(\frac{1+\sqrt{1+4z}}{2}\right)^{n+1} - \left(\frac{1-\sqrt{1+4z}}{2}\right)^{n+1} \right), \quad n \geqslant 0

进一步推广，来看看

B−1(z)n+(−z)nB2(−z)n\displaystyle \mathcal{B}_{-1}(z)^n + (-z)^n \mathcal{B}_2(-z)^n 是多少呢

同样根据之前的证明

当 k>nk > n 时
[zk](−z)nB2(−z)n=(−1)n[zk−n]B2(−z)n=(−1)n(−1)k−n[zk−n]B2(z)n\displaystyle [z^k] (-z)^n \mathcal{B}_2(-z)^n = (-1)^n [z^{k-n}] \mathcal{B}_2(-z)^n = (-1)^n (-1)^{k-n} [z^{k-n}] \mathcal{B}_2(z)^n

=(−1)k(2(k−n)+nk−n)n2(k−n)+n\displaystyle \quad = (-1)^k \binom{2(k-n) + n}{k-n} \frac{n}{2(k-n) + n}

=(−1)k(2k−nk−n)n2k−n\displaystyle \quad = (-1)^k \binom{2k-n}{k-n} \frac{n}{2k-n}

=(−1)k2k−nk−n(2k−n−1k−n−1)n2k−n=(−1)k(2k−n−1k−n−1)nk−n\displaystyle \quad = (-1)^k \frac{2k-n}{k-n} \binom{2k-n-1}{k-n-1} \frac{n}{2k-n} = (-1)^k \binom{2k-n-1}{k-n-1} \frac{n}{k-n}

=(−1)k(2k−n−1k)nk−n=(−1)(n−kk)nn−k\displaystyle \quad = (-1)^k \binom{2k-n-1}{k} \frac{n}{k-n} = (-1) \binom{n-k}{k} \frac{n}{n-k}

由此可以推出

k>nk > n 时
[zk](−z)nB2(−z)n=(−1)[zk]B−1(z)r\displaystyle [z^k](-z)^n \mathcal{B}_2(-z)^n = (-1) [z^k]\mathcal{B}_{-1}(z)^r

∑k⩽n(n−kk)nn−kzk=(1+1+4z2)n+(1−1+4z2)n,n⩾0\displaystyle \sum_{k \leqslant n} \binom{n-k}{k} \frac{n}{n-k} z^k = \left(\frac{1+\sqrt{1+4z}}{2} \right)^n + \left(\frac{1-\sqrt{1+4z}}{2} \right)^n, \quad n \geqslant 0