数论，生成函数，多项式（一）

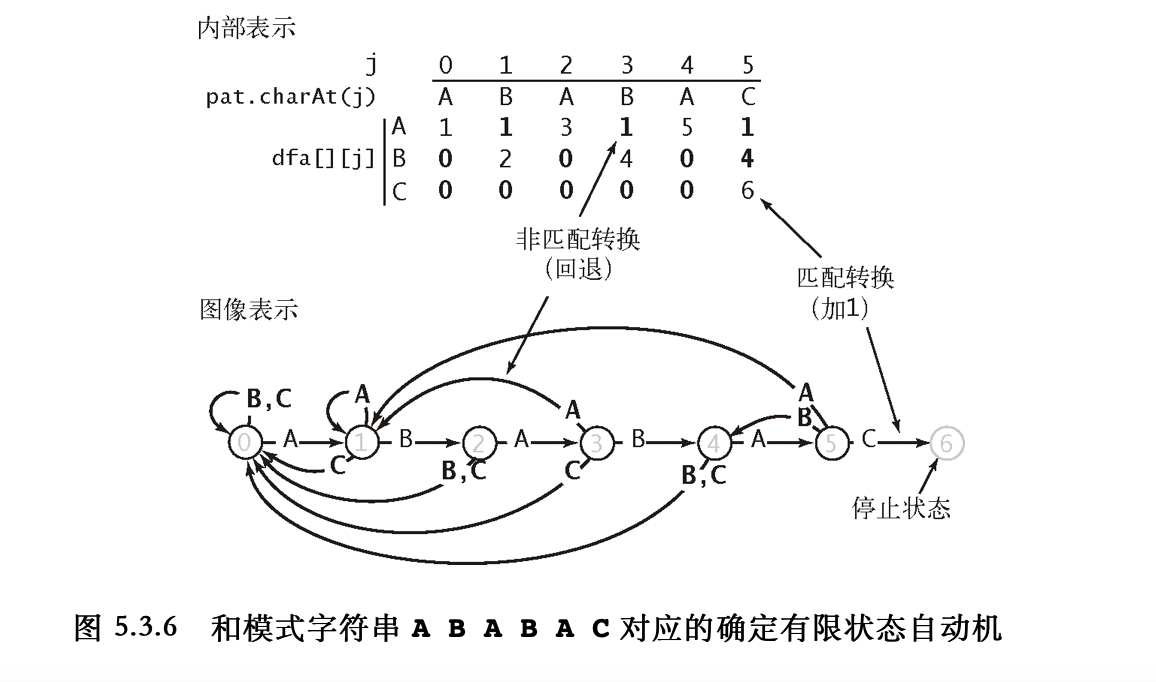
生成函数

斐波那契生成函数
将数列的项映射到多项式，就构成了最简单的生成函数，对于斐波那契数列 $F$

$\displaystyle F(x) = F_0 + F_1x + F_2x^2 + \cdots = \sum_{n \geqslant 0} F_nx^n$

$$\begin{aligned} F(x) = F_0 + F_1x + &F_2x^2 + F_3x^3 + F_4x^4 + F_5x^5 + \cdots \\ xF(x) =\quad F_0x + &F_1x^2 + F_2x^3 + F_3x^4 + F_4x^5 + \cdots \\ x^2F(x) = \quad \quad &F_0x^2 + F_1x^3 + F_2x^4 + F_3x^5 + \cdots \end{aligned}$$

注意到 $F_0 = 0$，并且 $F_i = F_{i-1} + F_{i-2}$
$F(x) - xF(x) - x^2F(x) = (F_1 - F_0)x = x$

生成函数为 $\displaystyle F(x) = \frac{x}{1 - x - x^2}$

熟练的话，根据递推 $a_n = a_{n-1} + a_{n-2}$ 可以推出
$\displaystyle [x^n]F(x) = x\cdot [x^{n-1}]F(x) + x^2 \cdot [x^{n-2}]F(x), \quad n \geqslant 2$
特别注意，此时序列不包括 $\left<x^0, x^1 \right>$ 的项，减去对应的项即可
$\displaystyle [x^n]F(x) - F_0 - F_1x = \left(x \cdot [x^{n-1}]F(x) - F_0x \right) + \left( x^2 \cdot [x^{n-2}]F(x) \right)$

即 $\displaystyle F(x) = xF(x) + x^2F(x) + (F_1 - F_0)x$

问题描述
用 $2 \times 1$ 的多米诺骨牌完全覆盖 $2 \times n$ 的矩形，有多少种不同的方式
设 $n = 0$ 时候的方案数为 $a_0$，$n = 1$ 方案数为 $a_1$，以此类推，那么将方案数 $a_i \to a_ix^{i}$
映射成多项式的系数，转为研究 $f(x) = \displaystyle\sum_{i = 1}^{n} a_ix^{i}$
$f(x)$ 称为序列 $\left<a_0, a_1, a_2, \cdots a_n \right>$ 的生成函数

不仅如此，序列 $\left<a_0, a_1, a_2, \cdots, a_n\right>$ 还可以表示斐波那契数，斯特林数，卡特兰数等等

以二项式举例，$\displaystyle \left<\binom{r}{0}, \binom{r}{1}, \binom{r}{2}, \cdots \right>$ 生成函数为

$(1+x)^{r} = \displaystyle\sum_{k \geqslant 0} \binom{r}{k} x^{k}$，同理，$(1+x)^{s} = \displaystyle\sum_{k \geqslant 0} \binom{r}{s} x^{s}$

令 $n \leftarrow r+s$，可以推出 $(1+x)^{r}(1+x)^{s} = (1+x)^{r+s}$，对应到生成函数，对应到数列第 $n$ 项 $x^n$ 的系数

$$\sum_{k \geqslant 0}^{n} \binom{r}{k} \binom{s}{n-k} = \binom{r+s}{n}$$

这就是范德蒙德卷积

回到一开始的问题
不妨记 $n$ 所对应的方案数为 $dp(n)$，那么根据第一列骨牌的摆放方式，可以竖着也可以横着
如果竖着放 $1$ 个骨牌，剩下的方案数对应 $dp(n-1)$，如果横着放 $2$ 个，方案数为 $dp(n-2)$
$dp(n) = dp(n-1) + dp(n-2)$，显然是一个斐波那契数列

斐波那契数对应 $a_0 = 1, a_1 = 1, a_2 = 1, a_{n} = a_{n-2} + a_{n-1}$，求出生成函数为
$f(x) = \displaystyle\frac{x}{1-x-x^2}$，原问题对应的方案数 $dp(n) = F_{n+1}$

记生成函数 $f(x)$ 中 $x^{n}$ 的系数为 $[x^{n}]f(x)$，那么有 $\displaystyle\frac{x}{1-x-x^2} = \sum_{k = 0}^{n} [x^{k}]f(x) \cdot x^{k}$

原问题对应 $x^{k} \leftarrow x^{k+1}$，那么有 $\displaystyle\frac{x}{1-x-x^2} = \sum [x^{k+1}]f(x)$，可以得到

$\displaystyle\frac{1}{1-x'-(x')^2} = \sum [{x'}^{k}]f(x')$，该问题的生成函数为 $f(x) = \displaystyle\frac{1}{1-x-x^2}$

多米诺骨牌问题

实际上，探讨 $3 \times n$ 的多米诺覆盖问题

根据是否允许使用竖着的牌，可以将方案数分为两类，一类是仅允许使用横着的骨牌，另一类是允许使用竖着的骨牌
这两种方案，分别对应到填满 $3 \times n$ 完整的矩形 $U_n$ ，和填满 $3 \times n$ 但缺一个角的矩形 $V_n$

如上图所示，有如下递推成立

$$\begin{aligned} &U_0 = 1, U_1 = 0 \\ &V_0 = 0, V_1 = 1 \\ &U_n = U_{n-2} + 2V_{n-1}, \ V_n = V_{n-2} + U_{n-1}, \ n \geqslant 2 \end{aligned}$$

求解生成函数
这一步用的策略也比较简单，假设说序列 $\left<a_n\right>$ 对应的生成函数是 $f(x)$，如果有 $b_n = a_{n-2}$
那么求解 $b_n$ 的生成函数 $g(x)$ 的时候，有 $g(x) = x^2 \cdot f(x)$，形式化表述为
$[x^n]g(x) = [x^{n-2}]f(x)$，即 $\displaystyle [x^{n-2}]\frac{g(x)}{x^2} = [x^{n-2}]f(x)$
于是有 $[x^{n-2}] g(x) = [x^{n-2}] \left(x^2f(x)\right)$，可以推出 $g(x) = x^2 f(x)$

首先，将多米诺骨牌的递推写成对所有 $n$ 的形式
$U_n = 2V_{n-1} + U_{n-2} + [n = 0], \quad V_n = U_{n-1} + V_{n-2}$
对应的生成函数有
$U(x) = 2xV(x) + x^2U(x) + 1, \quad V(x) = xU(x) + x^2V(x)$

根据等式可以推出 $\displaystyle U(x) = \frac{1-x^2}{1-4x^2 + x^4}, \ V(x) = \frac{x}{1-4x^2 + x^4}$

根据 $\displaystyle\frac{1}{1-4x^2 + x^4}$ 展开，是关于 $x^2$ 的幂级数

根据生成函数可以发现，$U(x)$ 是关于 $x^2$ 的，也就是说 $U_{2k+1} = 0$，$V(x)$ 是关于 $x^2 \cdot x$ 的，也就是说 $V_{2n} = 0$

展开生成函数
这里可以令 $\displaystyle W(x^2) = \frac{1}{1-4x^2+x^4}$，我们有 $U(x) = (1-x^2)W(x^2), \ V(x) = xW(x^2)$

如果令 $y = x^2$，那么 $(1-x^2)W(x^2) = W(y) - yW(y)$，对于 $y^n$，右边有 $[y^n]W(y) - y\cdot[y^{n-1}]W(y)$
左边呢？因为 $y^{n} = x^{2n}$，所以 $[x^{2n}]U(x) = [y^{n}]W(y) - y\cdot[y^{n-1}]W(y)$

所以我们有 $U_{2n} = W_{n} - W_{n-1}$，同理 $[x^{2n+1}]V(x) = [y^n]W(y)$，即 $V_{2n+1} = W_{n}$

那么研究 $W(x)$ 及其展开即可，$1-4x + x^2 = (1-\phi x)(1-\hat{\phi} x)$，求出 $\phi = 2+\sqrt{3}, \ \hat{\phi} = 2-\sqrt{3}$

由此，我们有 $\displaystyle V_{2n+1} = W_{n} = \frac{3+2\sqrt{3}}{6}(2+\sqrt{3})^n + \frac{3-2\sqrt{3}}{6}(2-\sqrt{3})^n$

$\displaystyle U_{2n} = W_n - W_{n-1} = \frac{3+\sqrt{3}}{6}(2+\sqrt{3})^n + \frac{3-\sqrt{3}}{6}(2-\sqrt{3})^n = \frac{(2+\sqrt{3})^n}{3-\sqrt{3}} + \frac{(2-\sqrt{3})^n}{3+\sqrt{3}}$

注意到 $\displaystyle\frac{(2-\sqrt{3})^n}{3+\sqrt{3}} \in (0, 1)$，关于 $U_{2n}$ 的表达式简化为

$U_{2n} = \displaystyle \left\lceil \frac{(2+\sqrt{3})^n}{3-\sqrt{3}} \right\rceil, \ n \geqslant 0$
正确的答案是取离 $U_{2n}$ 最近的整数得到

换零钱问题

付 $50$ 美分的方案数，假设必须使用 $1$ 美分，$5$ 美分，$1$ 角（$10$ 美分），$25$ 美分以及 $50$ 美分硬币支付
假设只允许使用 $1$ 美分的硬币，此时的方案数为 $P$
$\begin{aligned}\displaystyle P &= \not 1 + \left< 1 \right> + \left< 1 \right>\left< 1 \right> + \left< 1 \right>\left< 1 \right>\left< 1 \right> + \left< 1 \right>\left< 1 \right>\left< 1 \right>\left< 1 \right> + \cdots \\ &= \not 1 + \left< 1 \right> + \left< 1 \right> ^2 + \left< 1 \right> ^3 + \left< 1 \right> ^ 4 + \cdots \end{aligned}$

其中每一项表示用几个 $1$ 美分硬币，如果允许使用 $5$ 美分呢？
实际上，对于每一种方案，我们要乘以 $\displaystyle\binom{P}{1}$，每一种 $5$ 美分的选择方案，都可以对应到 $P$ 种 $1$ 美分的方案任意选一种

$5$美分的方案数记为 $N$，那么
$\displaystyle\begin{aligned} N &= P + \left< 5 \right> P + \left< 5 \right>\left< 5 \right> P + \left< 5 \right>\left< 5 \right>\left< 5 \right> P + \left< 5 \right>\left< 5 \right>\left< 5 \right>\left< 5 \right>P + \cdots \\ &= (\not 5 + \left< 5 \right> + \left< 5 \right> ^2 + \left< 5 \right> ^3 + \left< 5 \right> ^4 + \cdots) P \end{aligned}$

以此类推，$10$ 美分的方案记为 $D$，$25$ 美分的方案记为 $Q$，$50$ 美分的方案记为 $C$，注意这里的方案是向下兼容的
比如你能用 $10$ 美分的，也能用 $1$ 美分，$5$ 美分的，但不能够用 $25$ 美分的

$D = (\not{10} + \left< 10 \right> + \left< 10 \right>^2 + \left< 10 \right>^3 + \left< 10 \right>^4 + \cdots) N$
$Q = (\not{25} + \left< 25 \right> + \left< 25 \right>^2 + \left< 25 \right>^3 + \left< 25 \right>^4 + \cdots) D$
$C = (\not{50} + \left< 50 \right> + \left< 50 \right>^2 + \left< 50 \right>^3 + \left< 50 \right>^4 + \cdots) Q$

问题就转换成为求解 $C$ 中恰好值 $50$ 美分的项数
考虑使用生成函数，用 $x$ 替代 $\left< 1 \right>$，$x^{50}$ 替代 $\left< 50 \right>$，这样购买 $13$ 美分的方案数为
$(\left<1\right>^{13}), (\left<5\right>^1, \left<1\right>^8), (\left<5\right>^2, \left<1\right>^3), (\left<10\right>^1, \left<1\right>^3)$
对应的 $x^{13}$ 的系数是 $4$，综上所述
$\displaystyle P = 1+x+x^2+x^3+x^4+\cdots$
$\displaystyle N = (1+x^5+x^{10}+x^{15}+x^{20}+\cdots)P$
$\displaystyle D = (1+x^{10}+x^{20}+x^{30}+x^{40}+\cdots)N$
$\displaystyle Q = (1+x^{25}+x^{50}+x^{75}+x^{100}+\cdots)D$
$\displaystyle C = (1+x^{50}+x^{100}+x^{150}+x^{200}+\cdots)Q$

显然 $P_n = 1$，另外可以知道 $N_n = \lfloor n/5 \rfloor + 1$，$N_n$ 对应支付 $n$ 美分的方案数
可以使用的 $5$ 美分有 $(0, 1, 2, \cdots, \lfloor n/5 \rfloor)$ 个，$5$ 美分的方案数对应 $\lfloor n/5 \rfloor + 1$
剩下 $1$ 美分的方案数是唯一的

注意到 $1+x^m+x^{2m}+\cdots = 1/(1-x^{m})$，可以知道
$P = 1/(1-x)$
$N = P/(1-x^5)$
$D = N/(1-x^{10})$
$Q = D/(1-x^{25})$
$C = Q/(1-x^{50})$

可以化为
$P = 1+xP$
$N = P + x^5N$
$D = N + x^{10}D$
$Q = D + x^{25}Q$
$C = Q + x^{50}C$

展开生成函数，可以知道 $[x^n]P(x) = x \cdot [x^{n-1}]P(x) + [n = 0]$
$[x^n]N(x) = [x^n]P(x) + x^{5}\cdot [x^{n-5}]N(x)$，以此类推
$P_n = P_{n-1} + [n=0]$
$N_n = N_{n-5} + P_n$
$D_n = D_{n-10} + N_n$
$Q_n = Q_{n-25} + D_n$
$C_n = C_{n-50} + Q_n$

这样可以递归的来求，比如说 $Q_n = D_{n} + D_{n-25} + D_{n-50} + D_{n-75} + \cdots$

其实 $C_n$ 的封闭形式也很好求，注意到
$(1-x)P = 1$
$(1-x^5)N = P$
$(1-x^{10})D = N$
$(1-x^{25})Q = D$
$(1-x^{50})C = Q$

两边全部乘起来，得到 $C = \displaystyle\frac{1}{1-x}\frac{1}{1-x^5}\frac{1}{1-x^{10}}\frac{1}{1-x^{25}}\frac{1}{1-x^{50}}$

实际上，$\displaystyle\frac{1}{(1-x)(1-x^2)(1-x^3)\cdots}$ 中 $x^{n}$ 的系数为 $p(n)$，对应 $n$ 的划分的个数

$n$ 的一个划分，即将 $n$ 表示成正整数之和，不考虑顺序

生成函数展开策略

基本展开

二项式展开
二项式比较值得注意的恒等式有如下两种

$$\frac{1}{(1-x)^{n+1}} = \sum_{k \geqslant 0} \binom{n+k}{n} x^{k}$$

这个式子的证明也比较容易，可以通过反转上指标得到，反转上指标的公式如下
$\displaystyle \begin{aligned}r^{\underline{k}} &= r(r-1)\cdots (r-k+1) \\ &=(-1)^{k}(-r)(-r+1)\cdots (k-1-r) = (-1)^{k}(k-1-r)^{\underline{k}}\end{aligned}$
反转上指标的规则是

$$\binom{r}{k} = (-1)^{k} \binom{k-r-1}{k}$$

有了这个规则，实际上 $(1-x)^{-n-1}$ 的展开 $x^k$ 系数本来是 $\displaystyle(-1)^k\binom{-n-1}{k}$，反转上指标后 $\displaystyle \binom{n+k}{k}$
很容易得到上式

另外，如果将上述展开式两边同时 $\times x^{n}$，就得到以下推广

$$\frac{x^{n}}{(1-x)^{n+1}} = \sum_{k \geqslant 0} \binom{k}{n} x^{k}$$

待定系数展开
对于斐波那契生成函数 $f(x) = \displaystyle \frac{x}{1-x-x^2}$，分母二次式可以写成 $(1-\alpha x)(1-\beta x)$ 形式

$\displaystyle \frac{x}{1-x-x^2} = \frac{A}{1-\alpha x} + \frac{B}{1-\beta x}$，求解待定系数即可

接下来将 $\displaystyle\frac{A}{1-\alpha x} + \frac{B}{1-\beta x}$ 展开成幂级数，$\displaystyle \sum_{k \geqslant 0}a_k x^k$
对应的第 $k$ 项即为 $a_k = [x^{k}]f(x)$

展开求解，容易发现 $\alpha, \beta$ 分别是 $x^2-x+1=0$ 的两个根，$\alpha = \displaystyle\frac{1+\sqrt{5}}{2}, \beta = \frac{1-\sqrt{5}}{2}$
令 $\phi = \displaystyle\frac{1 + \sqrt{5}}{2}, \hat{\phi} = \displaystyle \frac{1-\sqrt{5}}{2}$，代入可知， $A = -B$，且 $A = \displaystyle\frac{1}{\sqrt{5}}$

综上所述，可以得到生成函数为 $\displaystyle f(x) = \frac{1}{\sqrt{5}}\left(\frac{1}{1-\phi x} - \frac{1}{1-\hat{\phi}x}\right)$

展开成幂级数，对于第 $n$ 项斐波那契数，通项为 $a_n = \displaystyle\frac{1}{\sqrt{5}} \left(\phi ^ n - \hat{\phi} ^ n\right)$

基本策略

$F(x), G(x)$ 分别为 $\left<f_n\right>, \left<g_n\right>$ 的生成函数，对于取负值的 $n$，令 $f_n, g_n$ 均为 $0$

线性和
$\displaystyle\alpha F(x)+\beta G(x) = \alpha \sum_{n} f_nx^n + \beta \sum_n g_n x^n = \sum_{n}(\alpha f_n + \beta g_n) x^n$
$\left< \alpha f_n + \beta g_n \right>$ 的生成函数就为 $\alpha F(x) + \beta G(x)$

向右平移 $m$ 位
构造 $\left<0, 0, \cdots, 0, g_0, g_1, \cdots \right> = \left< g_{n-m} \right>$，实际上，

$\displaystyle x^m G(x) = \sum_{n} g_n x^{n+m} = \sum_{n} g_{n-m} x^n, \quad m \geqslant 0$

向左平移 $m$ 位
我们需要减去前 $m$ 项，$\left< g_m, g_{m+1}, g_{m+2}, \cdots \right> = \left< g_{n+m} \right>$

$\displaystyle \frac{G(x)-g_0 - g_1x - \cdots - g_{m-1}x^{m-1}}{x^m} = \sum_{n \geqslant m} g_n x^{n-m} = \sum_{n \geqslant 0} g_{n+m} x^n$

这里因为 $g_0 = g_1 = \cdots = g_{m-1} = 0$，所以成立

常数倍
$\displaystyle G(cx) = \sum_{n}g_n(cx)^n = \sum_{n} c^n g_n x^n$
给出了 $\left< c^n g_n \right>$ 的生成函数

微分
$\displaystyle G'(x) = g_1 + 2g_2x + 3g_3 x^2 + \cdots = \sum_{n}(n+1)g_{n+1}x^{n}$
给出更普遍的形式

$\displaystyle xG'(x) = \sum_{n} n g_n x^n$，这是 $\left< ng_n \right>$ 的生成函数

积分
$\displaystyle\int_{0}^{x} G(t) {\rm d} t = g_0x + \frac{1}{2}g_1x^2 + \frac{1}{3} g_2x^3 + \cdots = \sum_{n \geqslant 1} \frac{1}{n} g_{n-1}x^n$

向左平移，给出 $\left< g_n / n \right>$ 的生成函数 $\displaystyle \int_{0}^{x} \left(\frac{G(t) - g_0}{t} \right) {\rm d} t$

卷积
$\displaystyle F(x)G(x) = \sum_{n} \left(\sum_{k} f_k g_{n-k}\right) x^n$
注意到 $k < 0$ 时 $f_k = 0$， $k > n$ 时 $g_{n-k} = 0$，所以有 $\left< f_n \right>, \left< g_n \right>$ 卷积生成函数

$\displaystyle \sum_{n}\left(\sum_{k = 0}^{n} f_k g_{n-k}\right)x^n = F(x)G(x)$

特殊卷积
取 $F(x) = x^m$，此时求和式只有一项 $f_m = 1$，其他的 $f$ 均为 $0$，所以 $\displaystyle \sum_{n} g_{n-m} x^n = x^m G(x)$

取 $F(x) = \displaystyle \frac{1}{1-x} = 1+x+x^2+\cdots$
此时所有的 $f$ 均为 $1$，我们有

$\displaystyle \frac{1}{1-x}G(x) = \sum_{n}\left(\sum_{k = 0}^{n}g_{n-k}\right)x^n = \sum_{n} \left(\sum_{k \geqslant n} g_k\right) x^n$

用 $1/(1-x)$ 乘以一个生成函数，得到原序列累加和数列的生成函数

常见的生成函数求解举例

$f_n = \left<1, 1, 1, \cdots \right> \longrightarrow \displaystyle \sum_{n} x^n = \frac{1}{1-x}$

基于此，我们很容易求出其他生成函数

$f_n = \left<1, 2, 3, \cdots \right> = 1 + 2x + 3x^2 + \cdots = \displaystyle\sum_{n}(n+1)\cdot \bm{1}\cdot x^n$
我们知道 $g_{n} = \left<1, 1, \cdots\right>$ 的生成函数是 $G(x) = \displaystyle \frac{1}{1-x}$

根据前面微分生成函数，可以知道 $f_n$ 的生成函数 $\displaystyle F(x) = G'(x) = \frac{1}{(1-x)^2}$

$f_n = \left<1, 0, 1, 0, \cdots \right>$
注意到该序列只有偶次幂有贡献，令 $x \leftarrow x^2$，$F(x) = \displaystyle \frac{1}{1-x^2}$

取给定数列标号为偶数的项，$\left<g_0, 0, g_2, 0, g_4, 0, \cdots \right>$ 有一般性的方法

$G(x) + G(-x) = \displaystyle \sum_{n} g_n \left(1 + (-1)^n \right) x^n = 2 \sum_{n} g_n [n \bmod 2 = 0] x^n$

$\displaystyle \frac{G(x)+G(-x)}{2} = \sum_{n} g_{2n}x^{2n}$

类似的，奇数项为

$\displaystyle \frac{G(x)-G(-x)}{2} = \sum_{n} g_{2n+1}x^{2n+1}$

比如对斐波那契数列偶数项 $\left<0, 1, 3, 8, \cdots \right>$ 求生成函数

$\displaystyle\sum_{n}F_{2n}x^{2n} = \frac{1}{2} \left(\frac{x}{1-x-x^2} + \frac{-x}{1+x-x^2} \right) = \frac{x^2}{1-3x^2 + x^4}$

递归式求解

多项式除法

形如 $\displaystyle R(x) = \frac{P(x)}{Q(x)}$

研究 $[x^n]R(x)$ 的形式，有一类有理函数，$\displaystyle \frac{a}{(1-\rho x)^{m+1}} = \sum_{n \geqslant 0} \binom{m+n}{m} a \rho ^n x^n$

这样可以构造出一个有限和式 $\displaystyle S(x) = \frac{a_1}{(1-\rho_1 x)^{m_1 + 1}} + \frac{a_2}{(1-\rho_2 x)^{m_2 + 1}} +\cdots + \frac{a_k}{(1-\rho_k x)^{m_k + 1}}$

展开之后，对于 $x^n$ 的系数有 $\displaystyle[x^n]S(x) = a_1 \binom{m_1 + n}{m_1} \rho_1 ^n + a_2 \binom{m_2 + n}{m_2} \rho_2 ^n + \cdots + a_k \binom{m_k + n}{m_k} \rho_k ^n$

要证明 $R(x)$ 为多项式，必须证明每一个 $R(0) \neq \infty$ 的有理函数 $R(x) = S(x) + T(x)$，其中 $T(x)$ 为多项式

注意到当 $x = 1/\rho_1, 1/\rho_2, \cdots, 1/\rho_k$ 的时候有 $S(x) = \infty$，而 $R(x) = S(x) + T(x)$ 为多项式
取 $\alpha_k = 1/\rho_k$，我们有 $\displaystyle\lim_{x_k \to \alpha_k} S(x) = S(\alpha_k) = \infty$
所以只要证 $\displaystyle\lim_{x_k \to \alpha_k} P(x)/Q(x) = \infty$

另一方面，$P, Q$ 是多项式，仅当 $Q(x) = 0$ 时有 $R(x) = \infty$
由此考虑 $\displaystyle\lim_{x_k \to \alpha_k} Q(x) = Q(\alpha_k) = 0, \ \alpha_k = 1/\rho_k$

对于 $Q(x) = q_0 + q_1x + q_2x^2 + \cdots + q_mx^m, \quad (q_0 \neq 0, q_m \neq 0)$，其反射多项式为
$Q^{R}(x) = q_0x^m + q_1x^{m-1} + \cdots + q_m$
二者的关系为 $Q^{R}(x) = q_0(x-\rho_1)\cdots (x-\rho_m), \quad Q(x) = q_0(1-\rho_1x)\cdots(1-\rho_mx)$
这样我们可以求出 $\rho$

不同根的有理展开

若 $R(x) = \displaystyle\frac{P(x)}{Q(x)}$，其中 $Q(x) = q_0(1-\rho_1x)\cdots (1-\rho_k x)$，并且 $\left<\rho_1, \rho_2, \cdots, \rho_k \right>$ 不同
如果 $P(x)$ 是次数小于 $k$ 的多项式，那么有

$$[x^n]R(x) = a_1\rho_1^n + \cdots + a_k \rho_k ^n, \quad \left(a_k = \frac{-\rho_k P(1/\rho_k)}{Q'(1/\rho_k)}\right)$$

证明，实际上只要证 $R(x) = P(x)/Q(x)$ 等于 $\displaystyle S(x) = \frac{a_1}{1-\rho_1 x} + \cdots + \frac{a_k}{1-\rho_k x}$
这一步是根据幂级数展开的等价式

只要证 $x \to \displaystyle \frac{1}{\rho_k}$，即 $x \to \alpha_k, \ (\alpha_k = 1/\rho_k)$ 时，有 $S(x) = R(x)$

我们希望能证明 $\displaystyle \lim_{x \to \alpha_k} (x - \alpha_k) R(x) = \lim_{x \to \alpha_k} (x-\alpha_k) S(x)$

$\displaystyle\lim_{x \to \alpha_k} S(x) = \lim_{x \to \alpha_k}\frac{a(x-\alpha_k)}{1- \rho_k x}$，这是一个 $\displaystyle\frac{0}{0}$ 极限

应用洛必达法则，可以知道 $\displaystyle\lim_{x \to \alpha_k} S(x) = \displaystyle -a_k /\rho_k$

另外，$\displaystyle\lim_{x \to \alpha_k} (x - \alpha_k) \frac{P(x)}{Q(x)} = P(\alpha_k) \lim_{x \to \alpha_k}\frac{x-\alpha_k}{Q(x)} = \frac{P(\alpha_k)}{Q'(\alpha_k)}$

最后一步同样用了洛必达法则，这样就证明了结论

推广
若 $R(x) = \displaystyle \frac{P(x)}{Q(x)}$，其中 $Q(x) = q_0 (1- \rho_1 x)^{d_1} \cdots (1- \rho_k x)^{d_k}$，而 $\left<\rho_1, \rho_2, \cdots, \rho_k \right>$ 互不相同

$P(x)$ 是次数小于 $d_1 + d_2 +\cdots + d_k$ 的多项式，那么有

$$[x^n]R(x) = f_1(n)\rho_1^n + \cdots + f_k(n)\rho_k^n, \quad n \geqslant 0$$

其中每一个 $f_k(n)$ 是一个次数为 $d_k - 1$ 并且首项系数为

$$a_k = \frac{(-\rho_k)^{d_k} P(1/\rho_k)d_k}{Q^{(d_k)}(1/\rho_k)} = \frac{P(1/\rho_k)}{(d_k-1)! q_0 \prod_{j \neq k} (1- \rho_j / \rho_k)^{d_j}}$$

类似地，实际上令 $\displaystyle S(x) = \frac{a_1(d_1 - 1)!}{(1- \rho_1 x)^{d_1}} + \cdots + \frac{a_k(d_k - 1)!}{(1- \rho_k x)^{d_k}}$

我们同样地，只要证 $\displaystyle \lim_{x \to \alpha_k}(x - \alpha_k)^{d_k} \frac{P(x)}{Q(x)} = \lim_{x \to \alpha_k}(x - \alpha_k)^{d_k}S(x)$

其中，$d_k = \max(d_1, d_2, \cdots, d_k)$

先证右边，根据洛必达法则，$\displaystyle\lim_{x \to \alpha_k}(x - \alpha_k)^{d_k} \cdot \frac{a_k(d_k - 1)!}{(1- \rho_k x)^{d_k}} = \frac{a_k(d_k-1)!}{(-\rho_k)^{d_k}}$

对于左边，$\displaystyle \lim_{x \to \alpha_k} (x-\alpha_k)^{d_k} \frac{P(x)}{Q(x)} = P(\alpha_k) \lim_{x \to \alpha_k} \frac{d_k (d_k-1)!}{Q^{(d_k)}(x)}$

从而 $\displaystyle \frac{a_k (d_k-1)!}{(-\rho_k)^{d_k}} = \frac{d_k (d_k-1)! P(\alpha_k)}{Q^{(d_k)}(\alpha_k)}$

举例，斐波那契数列
$P(x) = x, Q(x) = 1-x-x^2$，那么 $\rho = \phi = \displaystyle\frac{1+\sqrt{5}}{2}$，$\phi^n$ 的系数是 $\displaystyle\frac{-\rho P(1/\rho)}{Q'(1/\rho)} = \frac{\rho}{\rho+2}$

由此 $\phi^{n}$ 的系数是 $\displaystyle\frac{\phi}{\phi+2} = \frac{1}{\sqrt{5}}$，$\hat{\phi}^n$ 的系数是 $\displaystyle\frac{\hat{\phi}}{\hat{\phi}+2} = \frac{-1}{\sqrt{5}}$

$F_n = \displaystyle (\phi^n - \hat{\phi}^n) / \sqrt{5}$

带随机性的递归式

引入修正因子，比如

$$\begin{aligned} &g_0 = g_1 = 1 \\ &g_n = g_{n-1} + 2g_{n-2} + (-1)^n \quad n \geqslant 2 \end{aligned}$$

引入 $n < 2$ 的修正因子，$g_n = g_{n-1} + 2g_{n-2} + (-1)^n[n \geqslant 0] + [n=1]$

技巧，实际上 $(-1)^n[n\geqslant 0] = \displaystyle \sum_{n} \binom{-1}{n}x^n = (1+x)^{-1}$

可以推出 $\displaystyle G(x) = xG(x) + 2x^2G(x) + \frac{1}{1+x} + x$

$\displaystyle G(x) = \frac{1+x+x^2}{(1-2x)(1+x)^2}$

根据扩展定理，$\rho_1 = 2$，次数 $d_1 = 1$，$\rho_2 = -1$，次数 $d_2 = 2$
那么 $\rho_1 ^n$ 的系数 $f_1(n) = a_1$，$\rho_2 ^n$ 的系数为 $f_2(n) = a_2 n + C$

以求解 $a_2$ 为例，$1/\rho_2$ 代入展开公式，分子直接就是 $P(1/\rho_2) = 1+ 1/\rho_2 + (1/\rho_2)^2 = 1$
分母呢？分母为不包含 $d_2 = 2$ 次的项的乘积，用 $x = 1/\rho_2$ 代入，并且用 $(d_k-1)!$ 来除
$\displaystyle (2-1)!\cdot (1-2 \cdot 1/\rho_2) = 3$，这样 $1/3$ 就给出了 $\displaystyle n^{d_k-1}\rho_k^n$ 的系数
另外，取 $n= 0$，代入可以知道 $C = 2/9$

实际上，关于 $n$ 的系数表达式为 $Z(n) = \displaystyle\frac{7}{9} 2^n + \left(\frac{1}{3}n + C\right) (-1)^n$
$n = 0, Z(0) = 1$，求得

$\displaystyle g_n = \frac{7}{9}2^n + \left(\frac{1}{3}n +\frac{2}{9}\right) (-1)^n$

换零钱问题的封闭形式

多项式化简
$1-x^n = (1-x)(1+x+x^2+\cdots + x^{n-1})$

$\displaystyle C(x) = \frac{1}{1-x} \frac{1}{1-x^5} \frac{1}{1-x^{10}} \frac{1}{1-x^{25}} \frac{1}{1-x^{50}}$

实际上，$\displaystyle \frac{1}{1-x} = \frac{1+x+\cdots + x^4}{1-x^5}$

由此我们有 $C(x) = \displaystyle \frac{1+x+\cdots +x^4}{1-x^5} \frac{1}{1-x^{5}}\frac{1}{1-x^{10}}\frac{1}{1-x^{25}}\frac{1}{1-x^{50}}$

由此可得
$C(x) = (1+x+\cdots + x^4)\breve{C}(x^5)$，其中 $\displaystyle \breve{C}(x) = \frac{1}{1-x}\frac{1}{1-x} \frac{1}{1-x^{2}} \frac{1}{1-x^{5}} \frac{1}{1-x^{10}}$

下面考虑其封闭形式
注意到分母都是 $(1-x^{10})$ 的一个因子，所以

$\displaystyle \breve{C}(x) = \frac{A(x)}{(1-x^{10})^5}$，其中 $A(x) = A_0 + A_1x + \cdots + A_{31}x^{31}$

实际上，$\breve{C}(x) = \displaystyle \frac{1}{(1-x)^5} \frac{1}{(1+x)} \frac{1}{(1+x+x^2+x^3+x^4)} + \frac{1}{(1+x+\cdots + x^9)}$

$\breve{C}(x) = \displaystyle \frac{(1+x+\cdots +x^9)^4}{(1-x)^5(1+x+\cdots x^9)^5} \cdot \frac{1}{(1+x)} \frac{1}{(1+x+\cdots + x^4)}$

可以推出 $A(x) = \displaystyle \frac{(1+x+\cdots +x^9)^4}{(1+x + \cdots + x^4)(1+x)} = (1+x+\cdots x^9)^2 \cdot \frac{(1+x+\cdots +x^9)}{(1+x)} \frac{(1+x+\cdots +x^9)}{(1+x+\cdots + x^4)}$

所以， $A(x) = \displaystyle (1+x+\cdots + x^9)^2 (1+x+\cdots + x^8) (1+x^5)$

展开之后，对于 $A_r \cdot x^r$，幂指为 $x^r$ 对应的系数记为 $A_r$，由此构造出向量

$\displaystyle\bm{A}[0\cdots 31] = \left<\begin{aligned} &1, 2, 4, 6, 9, 13, 18, 24, 31, 39, 45, 52, 57, 63, 67, 69 \\ &69, 67, 63, 57, 52, 45, 39, 31, 24, 18, 13, 9, 6, 4, 2, 1 \end{aligned} \right>$

很惊奇地发现具有对称性，另外，根据二项式展开，$\displaystyle 1/(1-x)^5 = (1-x)^{-4-1} = \binom{4+k}{4}x^{k}$

对于 $\displaystyle \frac{1}{(1-x^{10})^5} = \sum_{k \geqslant 0} \binom{k+4}{4}x^{10k}$

那么对于 $n = 10q+r, \ 0 \leqslant r < 10$，可以确定系数 $\breve{C}_n = [x^n]\breve{C}(x)$

$\displaystyle \breve{C}_{10q+r} = \sum_{j, k} A_j \binom{k+4}{4} [10q+r = 10k+j]$

注意到如下成立
$\displaystyle\begin{aligned} &10q + r \\ &10(q-1) + r+10 \\ &10(q-2) + r+20 \\ &10(q-3) + r+30 \end{aligned}$

依次取 $k = \left<q, q-1, q-2, q-3 \right>$，可以有

$\displaystyle\breve{C}_{10q+r} = A_r \binom{q+4}{4} + A_{r+10} \binom{q+3}{4} + A_{r+20}\binom{q+2}{4} + A_{r+30} \binom{q+1}{4}$

那么要求 $50$ 美分的方案就简单了，实际上就是求 $C_{50q} = \breve{C}_{10q}$

$q=1, r=0$ 代入之后，$ans \leftarrow \displaystyle \binom{5}{4} + 45 \binom{4}{4} = 50$
$100$ 美分呢？$q= 2, r = 0$ 就可以算出来啦