tarjan 算法与连通性

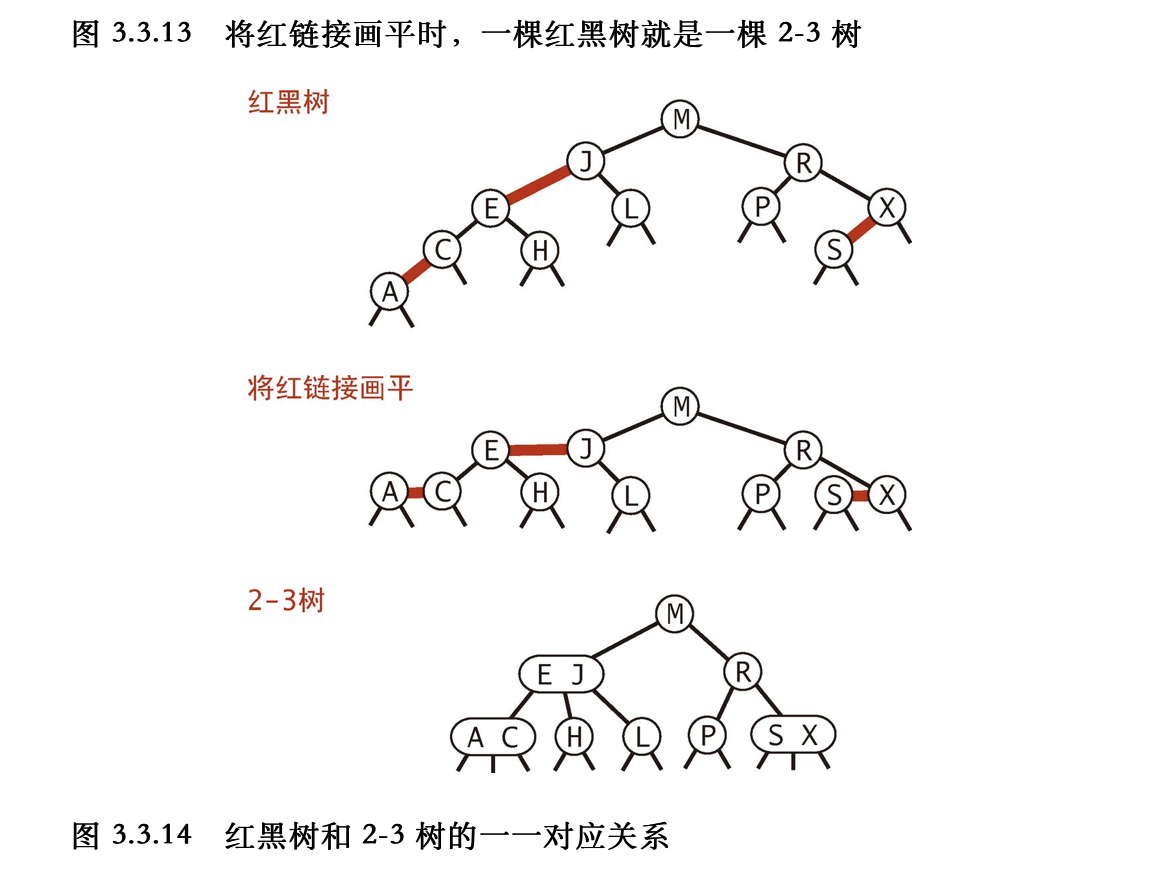
有向图的连通性

强连通分量$\textbf{SCC}$
图中任意两个节点 $x, y$，存在 $x \to y$ 的路径，也存在 $y \to x$ 的路径

在 $\text{dfs}(x)$ 的时候，用 $\text{dfn}(x)$ 记录 $x$ 第一次被访问的时候的时间戳，即点刚被发现的时间
用 $\text{sub}(x)$ 记录以 $x$ 为根的子树，$\text{low}(x)$ 记录 $\text{sub}(x)$ 中可以到达（追溯到）的，最早被发现的点
$\text{low}(x) = \displaystyle\min \{\text{dfn}(u) \mid u \in \text{sub}(x)\}$

对边 $(x, y)$ 进行分类，在 $\text{dfs}(x)$ 时有如下性质

• 树边，即深度优先搜索森林中的边，$\text{dfn}(y) = 0$，此时发生递归访问 $\text{dfs}(y)$
  递归访问之后，此时 $\text{low}(y)$ 用来更新 $\text{low}(x)$
• 后向边，如图中所示，此时有环，并且 $\text{dfn}(y) < \text{dfn}(x)$
  注意到此时环上所有节点相互可达，环中所有节点的 $\text{low}(u)$ 值会被 $\text{dfn}(y)$ 更新
  $\text{low}(u) \leftarrow \min(\text{low}(u), dfn(y))$
• 前向边，$y$ 为 $x$ 的后代，这条边对强连通分量以及是否成环没有贡献，因为本来就有 $x \to y$ 的路径
• 横叉边，不一定有环，如果存在环，说明 $\text{dfs}(y)$ 的时候找到了 $(y, \text{anc}(x))$ 的边，$\text{anc}(x)$ 为 $x$ 的祖先
  不妨令 $u \leftarrow \text{anc}(x)$，那么在 $\text{dfs}$ 执行 $x$ 所在的分支的时候，$(fa(u), u)$ 这条边
  有 $\text{dfn}(u) < \text{dfn}(fa(u))$，这条边为后向边

根据上面分析，只需要把横叉边和后向边统一成一个块即可

性质 1 考虑强连通分量 $C$，设其中第一个被发现的节点为 $u$，那么 $C$ 中的其他节点都是 $u$ 的后代
如果我们维护一个栈，当 $u$ 的所有分支都被搜索完毕的时候，立刻返回栈中所有元素并清空栈
那么栈中所有的元素和 $u$ 都同属于一个强连通分量

算法设计 定义追溯值，用栈维护当前环 $C$ 中的节点
$\bm{low}(u)$ 维护 $u$ 能够追溯到的最早的点，这个最早点必须满足以下特征
首先 $\text{low}(u)$ 追溯到的最早点 必须在栈中
其次存在从 $\text{sub}(u)$ 出发的有向边，能够返回到这个最早点
简而言之，$\text{low}(u)$ 就是从 $\text{sub}(u)$ 出发，在当前栈中能够追溯到的 $\text{dfn}$ 最小的（最早被发现）的点

性质 2 $u$ 是 $C$ 中最先被发现的点，当且仅当 $\text{low}(u) = \text{dfn}(u)$
此时 $u$ 及其所在的块都被搜完了，标记栈中所有元素属于一个强连通分量 $C$，然后清空栈

可以设计出如下算法

• $\text{dfs}(x)$ 的时候，$x$ 第一次被访问，此时 $\text{dfn}(x) = \text{low}(x) = ++time$
• 检查每一条边 $(x, y)$
  • $\text{dfn}(y) = 0$，递归访问 $dfs(y)$，回溯的时候 $\text{low}(y)$ 也已经计算出来了
    令 $\text{low}(x) = \min (\text{low}(x), \text{low}(y))$
  • $\text{dfn}(y) \neq 0$，如果 $y$ 在栈中，说明 $(x, y)$ 是后向边，$\text{low}(u) = \min(\text{low}(u), \text{dfn}(y))$
    $y$ 不在栈中，说明 $y$ 所在的分支已经处理完了，不用管 $y$
• 如果 $\text{low}(x) = \text{dfn}(x)$，说明 $x$ 是 $C$ 中第一个被发现的点，并且 $x$ 所在的块都被搜完了
  栈中 $[S[top] \to x]$ 这些节点属于一个新的连通分量 $C$ , 标记这些元素并弹出，直到 $x$ 出栈

算法实现时候有两个细节

• 对于树边 $\text{dfn}(y) = 0$, 此时 $y \in \text{sub}(x)$，$\text{low}(y)$ 追溯到的集合 $\text{low}(x)$ 也可以追溯到
  所以令 $\text{low}(x) = \min(\text{low}(x), \text{low}(y))$
• 而对于后向边或者横叉边，此时 $\text{dfn}(y) \neq 0$ 并且 $y$ 在栈中，这个时候应该用 $\text{dfn}(y)$ 去更新 $\text{low}(u)$
  为什么呢？因为此时 $y$ 可能是当前环 $C$ 与其他环 $C'$ 的公共点，可能 $\text{low}(y) \in C'$，追溯最早点可能并不在当前环中
  并不能用 $\text{low}(y)$ 去更新 $\text{low}(x)$，而根据前面的分析，我们要找到当前环 $C$ 中第一个被发现的点
  令 $\text{low}(x) = \min(\text{low}(x), \text{dfn}(y))$

$\text{Tarjan}$ 算法还可以用来判环，因为执行 $\text{tarjan}$ 的时候，记录了强连通分量的个数 $\text{cnt}$
有向图无环，等价于 $\text{tarjan}$ 的过程中，对于任意节点 $u$，$u$ 只能和自身构成强连通分量
如果 $\text{cnt} = n$，那么说明图是一个 $\text{DAG}$

const int maxn = 1e4 + 10;
int n, m;
vector<int> G[maxn];

int cnt = 0;
vector<int> bl(maxn, 0);
vector<int> scc[maxn];
void getSCC() {
    cnt = 0;

    vector<int> dfn(maxn, 0), low(maxn, 0);
    stack<int> stk;
    vector<int> inq(maxn, 0);

    int tim = 0;
    function<void(int)> tarjan = [&](int x) {
        dfn[x] = low[x] = ++tim;
        stk.push(x), inq[x] = 1;

        for (auto y : G[x]) {
            if (!dfn[y]) {
                tarjan(y);
                low[x] = min(low[x], low[y]);
            }
            else if (inq[y]) {
                low[x] = min(low[x], dfn[y]);
            }
        }
        if (low[x] == dfn[x]) {
            cnt++; int u;

            do {
                u = stk.top();
                stk.pop(), inq[u] = 0;
                bl[u] = cnt, scc[cnt].push_back(u);
            } while (u != x);
        }
    };


    for (int i = 1; i <= n; i++) if (!dfn[i]) {
        tarjan(i);
    }
}

void init() {
    for (int i = 0; i < maxn; i++) G[i].clear(), scc[i].clear();
}

int main() {
    freopen("input.txt", "r", stdin);
    cin >> n >> m;
    init();

    for (int i = 0; i < m; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        G[x].push_back(y);
    }
    
    getSCC();

    int k;
    scanf("%d", &k);
    for (int i = 0; i < k; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        int res = bl[x] == bl[y] ? 1 : 0;
        res ? printf("Yes") : printf("No");

        if (i != k-1) printf("\n");
    }
}

和强连通分量相关的问题，经常需要缩点，缩点的代码实现如下

vector<int> G0[maxn];

void shrink() {
    for (int x = 1; x <= n; x++) {
        for (auto y : G[x]) {
            if (bl[x] == bl[y]) continue;
            G0[bl[x]].push_back(bl[y]);
        }
    }
}

tarjan 判断 DAG

有了上述概念，可以用 $\text{tarjan}$ 算法判断一个图是否为 $\text{DAG}$ 并进行拓扑排序
第一次 $\text{dfs}$ 到某个点 $x$ 的时候标记 $vis(x) = 1$，当 $x$ 回溯完毕时标记 $vis(x) = 2$

$vis(x) = 1$ 表示这个点正在被访问，$vis(x) = 2$ 表示这个点回溯完毕，此时 $x$ 和它的子树 $\text{sub}(x)$ 都搜完了
并且 $x \cup \text{sub}(x)$ 没有环

$\text{dfs}(x)$ 的时候对于 $(x, y)$，如果 $vis(y) = 1$，那么一定有环
如果 $vis(y) = 2$ 说明是横叉边，可以不用管
当 $vis(y) = 0$ 的时候，说明 $(x, y)$ 是树边，那么继续搜 $\text{dfs}(y)$，看一下 $y$ 以及其子树有没有环

当一个点回溯完成，也就是 $vis(x) = 2$ 的时候，将其放入拓扑序列中，因为是模拟回溯过程
所以最后 $\text{vector}$ 中的顺序是 $n, n-1, \cdots, 1$，$\text{reverse}$ 一下才是真的拓扑序

vector<int> vec;
int n;
bool topo() {
    vector<int> vis(maxn, 0);

    function<bool(int)> dfs = [&](int x) {
        vis[x] = 1;
        for (auto y : G[x]) {
            if (vis[y] == 1) return false;
            else if (!vis[y] && dfs(y) == false) return false;
        }
        vis[x] = 2, vec.push_back(x);
        return true;
    };

    for (int i = 1; i <= n; i++) if (!vis[i]) {
        if (!dfs(i)) return false;
    }
    reverse(vec.begin(), vec.end());
    return true;
}

无向图的连通性

追溯值
$x$ 节点的追溯值，在无向图中指不通过搜索树上的边能够找到的最早节点
$\text{low}(u)$ 表示 $u$ 节点的追溯值，简单来说它是能找到的最早被发现的节点，简称为最早点
这个最早点必须满足以下条件
首先最早点必须在 $\text{sub}(u)$ 中，其次，通过 $1$ 条非搜索树边，能够连到 $\text{sub}(u)$ 中的点

$\text{low}(x)$ 的计算

• $\text{dfs}(x)$，第一次访问到 $x$ 的时候，令 $\text{low}(x) = \text{dfn}(x) = ++tim$
• 对于边 $(x, y)$，如果是树边，即 $\text{dfn}(y) = 0$，那么 $y$ 能追溯到的 $x$ 也可以追溯到
  令 $\text{low}(x) = \min(\text{low}(x), \text{low}(y))$
  如果 $\text{dfn}(y) \neq 0$，那么 $(x, y)$ 非树边，此时要用 $\text{dfn}(y)$ 来更新 $\text{low}(x)$
  实际上，$\text{low}(x)$ 的定义就是 $x$ 能通过非树边找到的最早点，令 $\text{low}(x) = \min(\text{low}(x), \text{dfn}(y))$

桥

无向图中的边 $(x, y)$ 是桥，当且仅当删除 $(x, y)$ 后，无向图是非连通图
此时 $\text{dfn}(x) < \text{low}(y)$，此外还有一些性质

• 桥一定是搜索树中的边，否则的话，删去这条非树边，任意两点 $x, y$ 仍然可以通过搜索树连通
  与桥的定义矛盾
• 任意一个简单环中的边都不是桥，因为删除任意一条边，对于简单环，图依然是连通的

根据以上分析，在 $\text{dfs}(x)$ 时，当 $\text{dfs}(y)$ 发生回溯时，根据 $\text{dfn}(x) < \text{low}(y)$ 判断 $(x, y)$ 是否为桥
此外还有一些问题，对于桥而言，一定是树边
$\text{dfs}(fa)$ 执行到边 $(fa, x)$ 并继续往下递归，由于是无向图，一定会检查到 $(x, fa)$，此时 $(x, fa)$ 是树边
不能够用 $\text{dfn}(fa)$ 来更新 $\text{low}(x)$，那如果有重边咋办？
如果有 $(fa, x)$ 的重边，除了第一条搜索树边之外，剩下的都是非树边，此时 $(fa, x)$ 一定不是桥
这时候 $(x, fa)$ 除了第一条边之外，都不是树边，可以用 $\text{dfn}(fa)$ 来更新 $\text{low}(x)$

在 $\text{dfs}$ 的时候只需要记录前向弧编号，$\text{dfs}(x, id)$，其中 $id$ 表示进入 $x$ 的前向弧
存无向图的时候，因为成对存储，检查从 $x$ 出发的每一条边 $i = (x, y)$，如果 $\text{dfn}(y) \neq 0$
只有当 $i \neq id \oplus 1$ 的时候，才执行 $\text{low}(x) = \min(\text{low}(x), \text{dfn}(y))$

using namespace Graph;
vector<int> bridge(maxn, 0);
void getBridge() {
    vector<int> dfn(maxn, 0), low(maxn, 0);
    int tim = 0;

    function<void(int, int)> tarjan = [&](int x, int id) {
        dfn[x] = low[x] = ++tim;
        for (int i = h[x]; i; i = ne[i]) {
            int y = ver[i];
            if (!dfn[y]) {
                tarjan(y, i);
                low[x] = min(low[x], low[y]);

                if (dfn[x] < low[y]) bridge[i] = bridge[i^1] = 1;
            }
            else if (i != (id ^ 1)) {
                low[x] = min(low[x], dfn[y]);
            }
        }
    };

    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) tarjan(i, 0);
    }
    for (int i = 2; i <= idx; i += 2) if (bridge[i]) {
        printf("%d %d\n", ver[i^1], ver[i]);
    }
}

割顶

$u$ 是无向图 $G$ 的割顶，当且仅当 $u$ 存在一个子节点 $v$
使得 $\text{sub}(v)$ 中没有反向边连回 $u$ 的祖先（连回 $u$ 不算）
$x$ 是割顶，当且仅当搜索树上存在子节点 $y$，满足 $\text{dfn}(x) \leqslant \text{low}(y)$

特别地，如果 $x$ 是根节点要特判，此时 $x$ 如果是割顶当且仅当树上至少两个节点 $y_1, y_2$ 满足条件

vector<int> cut(maxn, 0);
void getCut() {
    vector<int> dfn(maxn, 0), low(maxn, 0);
    int tim = 0;

    function<void(int, const int)> tarjan = [&](int x, const int root) {
        dfn[x] = low[x] = ++tim;
        int fl = 0;
        for (int i = h[x]; i; i = ne[i]) {
            int y = ver[i];
            if (!dfn[y]) {
                tarjan(y, root);
                low[x] = min(low[x], low[y]);

                if (low[y] >= dfn[x]) {
                    fl++;
                    if (x != root || (x == root && fl >= 2)) cut[x] = 1;
                }
            }
            else low[x] = min(low[x], dfn[y]);
        }
    };

    for (int i = 1; i <= n; i++) if (!dfn[i]) {
        tarjan(i, i);
    }
    for (int i = 1; i <= n; i++) if (cut[i]) {
        printf("%d ", i);
    }
    printf("\n");
}

边双连通分量

无向图不存在桥，称为边双连通图，极大边双连通图称为边双连通分量

无向图是边双连通图，当且仅当任意一条边都包含在至少一个简单环中（简单环即不自交的环）

算法
只需要删除桥边，然后 $\text{dfs}$ 找连通块即可，具体来说
先执行 $\text{tarjan}$ 算法标记桥，然后执行 $\text{dfs}(x)$，从 $x$ 出发不经过桥边
划分出连通块即可

vector<int> bl(maxn, 0);
void geteDCC() {
    fill(bl.begin(), bl.end(), 0);
    int num = 0;
    function<void(int)> dfs = [&](int x) {
        bl[x] = num;
        for (int i = h[x]; i; i = ne[i]) {
            int y = ver[i];
            if (bl[y] || bridge[i]) continue;
            dfs(y);
        }
    };

    for (int i = 1; i <= n; i++) {
        if (!bl[i]) {
            num++;
            dfs(i);
        }
    }

    printf("There are %d e-DCCs.\n", num);
    for (int i = 1; i <= n; i++) printf("%d belongs to DCC %d.\n", i, bl[i]);
}

缩点
将桥边 $(x, y)$ 看作是连接连通分量为 $\text{bl}(x)$ 和 $\text{bl}(y)$ 的树边
可以得到 $\text{eDCC}$ 森林

struct Edge {
    int ver;
};
vector<Edge> edges;
vector<int> G[maxn];

void addCC(int x, int y) {
    edges.push_back(Edge{y});
    G[x].push_back(edges.size()-1);
}
void shrink() {
    for (int i = 1; i <= idx; i++) {
        int x = ver[i^1], y = ver[i];
        if (bl[x] == bl[y]) continue;
        addCC(bl[x], bl[y]);
    }
    printf("After shink:\n");
    for (int i = 0; i < (int)edges.size(); i += 2) {
        printf("%d %d\n", edges[i^1].ver, edges[i].ver);
    }
}

点双连通分量

无向图不存在割顶，这样的子图称为点双连通图，极大点双连通子图称为点双连通分量

无向图是点双连通图，当且仅当满足以下条件之一
图的顶点数 $\leqslant 2$，或者是图中任意两点都同时包含在至少一个简单环中

证明如下，如果任意两点 $x, y$ 都包含在至少一个简单环中，$x \to y$ 有至少 $2$ 条不相交的路径
不论删除图中除了 $x, y$ 外的哪个节点，$x, y$ 总能通过 $2$ 条路径的其中一条相连
再证明必要性，假设一张图是点双连通图，并且 $x, y$ 不同时处于一个简单环中
如果 $x, y$ 间只有一条路径，那么这条路径上至少有一个割顶，与双连通图矛盾
如果 $x, y$ 有两条以上的路径，$x, y$ 之间又没有简单环，那么 $x, y$ 之间的路径会相交于一点 $p$
形成一个类似 twist 的拓扑结构，此时 $p$ 是一个割顶，与点双连通图矛盾

性质
如果一个点为孤立点，那么它自己就是一个 $\text{vDCC}$，除了孤立点之外，$\text{vDCC}$ 大小至少为 $2$
和边双连通分量对比，桥不属于任何一个 $\text{eDCC}$，但是割顶可能属于多个 $\text{vDCC}$