最短路径算法
SPFA
SPFA 算法是基于 Bellman-ford \text{Bellman-ford} Bellman-ford for i = 1 to ∣ G . V ∣ − 1 \textbf{for} \ i = 1 \ \textbf{to} \ |G.V|-1 for i = 1 to ∣ G . V ∣ − 1 for each edge ( u , v ) ∈ G . E : Relax ( u , v , w ) \quad \textbf{for} \ \text{each edge}(u, v) \in G.E: \quad \text{Relax}(u, v, w) for each edge ( u , v ) ∈ G . E : Relax ( u , v , w ) for each edge ( u , v ) ∈ G . E \textbf{for} \text{ each edge}(u, v) \in G.E for each edge ( u , v ) ∈ G . E if v . d > u . d + w ( u , v ) : return FALSE \quad \textbf{if} \ v.d > u.d + w(u, v): \quad \text{return FALSE} if v . d > u . d + w ( u , v ) : return FALSE return TRUE \text{return TRUE} return TRUE
证明,定义最短路径权重 路径 p = [ v 0 , v 1 , ⋯ , v k ] p = [v_0, v_1, \cdots, v_k] p = [ v 0 , v 1 , ⋯ , v k ] w ( p ) = ∑ i = 1 k w ( v i − 1 , v i ) w(p) = \displaystyle \sum_{i=1}^{k} w(v_{i-1}, v_i) w ( p ) = i = 1 ∑ k w ( v i − 1 , v i )
δ ( u , v ) = { min { w ( p ) : u → p v } 如果存在一条从 u 到 v 的路径 + ∞ \delta(u, v) = \begin{cases}
\min \{w(p): u \xrightarrow{p} v \} && \text{如果存在一条从 u 到 v 的路径} \\
+\infty
\end{cases}
δ ( u , v ) = { min { w ( p ) : u p v } + ∞ 如果存在一条从 u 到 v 的路径
结论 ,bellman-ford \text{bellman-ford} bellman-ford TRUE \text{TRUE} TRUE G G G
对于 ( u , v ) ∈ E , δ ( s , v ) ⩽ δ ( s , u ) + w ( u , v ) , s (u, v) \in E, \quad \delta(s, v) \leqslant \delta(s, u) + w(u, v), s ( u , v ) ∈ E , δ ( s , v ) ⩽ δ ( s , u ) + w ( u , v ) , s
bellman-ford \text{bellman-ford} bellman-ford ∀ ( u , v ) ∈ E \forall (u, v) \in E ∀ ( u , v ) ∈ E v . d = δ ( s , v ) ⩽ δ ( s , u ) + w ( u , v ) = u . d + w ( u , v ) v.d = \delta(s, v) \leqslant \delta(s, u) + w(u, v) = u.d + w(u, v)
v . d = δ ( s , v ) ⩽ δ ( s , u ) + w ( u , v ) = u . d + w ( u , v )
现在假定图 G G G s s s c = ⟨ v 0 , v 1 , ⋯ , v k ⟩ c=\langle v_0, v_1, \cdots , v_k \rangle c = ⟨ v 0 , v 1 , ⋯ , v k ⟩ v 0 = v k v_0 = v_k v 0 = v k ∑ i = 1 k w ( v i − 1 , v i ) < 0 \sum_{i=1}^{k} w(v_{i-1}, v_i) < 0
i = 1 ∑ k w ( v i − 1 , v i ) < 0
假设环路存在的情况下,bellman-ford \text{bellman-ford} bellman-ford TRUE \text{TRUE} TRUE v i . d ⩽ v i − 1 . d + w ( v i − 1 , v i ) v_{i}.d \leqslant v_{i-1}.d + w(v_{i-1}, v_i) v i . d ⩽ v i − 1 . d + w ( v i − 1 , v i ) i = 1 , 2 , ⋯ , k i = 1, 2, \cdots , k i = 1 , 2 , ⋯ , k ∑ i = 1 k v i . d ⩽ ∑ k = 1 k ( v i − 1 . d + w ( v i − 1 , v i ) ) = ∑ i = 1 k v i − 1 . d + ∑ i = 1 k w ( v i − 1 , v i ) \sum_{i=1}^{k} v_i.d \leqslant \sum_{k=1}^{k} (v_{i-1}.d + w(v_{i-1}, v_i)) = \sum_{i=1}^{k} v_{i-1}.d + \sum_{i=1}^{k} w(v_{i-1}, v_i)
i = 1 ∑ k v i . d ⩽ k = 1 ∑ k ( v i − 1 . d + w ( v i − 1 , v i ) ) = i = 1 ∑ k v i − 1 . d + i = 1 ∑ k w ( v i − 1 , v i )
注意到 v 0 = v k v_0 = v_k v 0 = v k ∑ i = 1 k v i . d = ∑ i = 1 k v i − 1 . d \sum_{i=1}^{k} v_i.d = \sum_{i=1}^{k} v_{i-1}.d
i = 1 ∑ k v i . d = i = 1 ∑ k v i − 1 . d
从而 0 ⩽ ∑ k = 1 k w ( v i − 1 , v i ) 0 \leqslant \displaystyle \sum_{k=1}^{k}w(v_{i-1}, v_i) 0 ⩽ k = 1 ∑ k w ( v i − 1 , v i )
SPFA算法实现 ,思想是一个点可能出队,入队多次 inq [ ⋯ ] \textbf{inq}[\cdots] inq [ ⋯ ] cnt \text{cnt} cnt cnt ( x ) \text{cnt}(x) cnt ( x ) δ ( s , x ) \delta(s, x) δ ( s , x ) cnt ( s ) = 0 \text{cnt}(s) = 0 cnt ( s ) = 0 d ( y ) ← d ( x ) + z d(y) \leftarrow d(x) + z d ( y ) ← d ( x ) + z cnt ( y ) = cnt ( x ) + 1 \text{cnt}(y) = \text{cnt}(x) + 1 cnt ( y ) = cnt ( x ) + 1 cnt ( y ) ⩾ n \text{cnt}(y) \geqslant n cnt ( y ) ⩾ n
分层图解决有后效性 dp
Telephone Lines
利用动态规划的思想,d p ( x , p ) dp(x, p) d p ( x , p ) 1 → x 1 \to x 1 → x p p p
( x , y ) (x, y) ( x , y ) d p ( y , p ) = min ( d p ( y , p ) , max ( d p ( x , p ) , z ) ) dp(y, p) = \min(dp(y, p), \max(dp(x, p), z)) d p ( y , p ) = min ( d p ( y , p ) , max ( d p ( x , p ) , z ) ) z = w ( x , y ) z = w(x, y) z = w ( x , y ) ( x , y ) (x, y) ( x , y ) d p ( y , p + 1 ) = d p ( x , p ) dp(y, p+1) = dp(x, p) d p ( y , p + 1 ) = d p ( x , p )
观察状态转移方程发现,存在转移d p ( x , p ) → z d p ( y , p ) , d p ( x , p ) → d p ( y , p + 1 ) dp(x, p) \xrightarrow{z} dp(y, p), \ dp(x, p) \to dp(y, p+1) d p ( x , p ) z d p ( y , p ) , d p ( x , p ) → d p ( y , p + 1 )
如果仅有 d p ( x , p ) → d p ( y , p + 1 ) dp(x, p) \to dp(y, p+1) d p ( x , p ) → d p ( y , p + 1 ) dp \text{dp} dp d p ( x , p ) → z d p ( y , p ) → ⋯ d p ( y k , p ) → z k d p ( x , p ) dp(x, p) \xrightarrow{z} dp(y, p) \to \cdots dp(y_k, p) \xrightarrow{z_k} dp(x, p) d p ( x , p ) z d p ( y , p ) → ⋯ d p ( y k , p ) z k d p ( x , p ) 环路 ,不符合 dp \text{dp} dp 有向无环图 的条件
但可以利用 spfa \text{spfa} spfa ( x , p ) , ( y , p ) (x, p), (y, p) ( x , p ) , ( y , p ) z z z ( x , p ) , ( y , p + 1 ) (x, p), (y, p+1) ( x , p ) , ( y , p + 1 ) 0 0 0 ( 1 , 0 ) (1, 0) ( 1 , 0 ) spfa \text{spfa} spfa d ( u ) = ∞ d(u) = \infty d ( u ) = ∞ ( u , v , z ) (u, v, z) ( u , v , z ) d ( v ) = min ( d ( v ) , max ( d ( u ) , z ) ) d(v) = \min (d(v), \max (d(u), z)) d ( v ) = min ( d ( v ) , max ( d ( u ) , z ) ) d ( n , K ) d(n, K) d ( n , K )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 const int maxn = 2e6 + 10, inf = 0x3f3f3f3f; const int maxm = 5e6 + 10; int n, m, K; namespace Graph { int idx = 1; int head[maxn], ver[maxm], e[maxm], ne[maxm]; void initG idx = 1; memset(head, 0, sizeof head); } void add(int a, int b, int c) { ver[++idx] = b, e[idx] = c, ne[idx] = head[a], head[a] = idx; } } using namespace Graph; inline int get(int x, int y) { return x + n*y; } int d[maxn], inq[maxn]; void spfa(int s) { queue<int> q; memset(d, inf, sizeof d); memset(inq, 0, sizeof inq); d[s] = 0, inq[s] = 1; q.push(s); while (q.size()) { auto u = q.front(); q.pop(); inq[u] = 0; for (int i = head[u]; i; i = ne[i]) { int v = ver[i]; if (d[v] > max(d[u], e[i])) { d[v] = max(d[u], e[i]); if (!inq[v]) q.push(v), inq[v] = 1; } } } } int main freopen("input.txt" , "r" , stdin); scanf("%d%d%d" , &n, &m, &K); initG(); while (m--) { int a, b, l; scanf("%d%d%d" , &a, &b, &l); for (int i = 0; i <= K; i++) { int u = get(a, i), v = get(b, i); add(u, v, l), add(v, u, l); } for (int i = 0; i < K; i++) { add(get(a, i), get(b, i+1), 0); add(get(b, i), get(a, i+1), 0); } } spfa(get(1, 0)); int ans = d[get(n, K)]; if (ans == inf) puts("-1" ); else printf ("%d\n" , ans); }
spfa 和 dp
spfa 的思想和 dp 有很类似的地方,dp 中的状态转移方程 d p ( y ) = d p ( x ) + f ( x , y ) dp(y) = dp(x) + f(x, y) d p ( y ) = d p ( x ) + f ( x , y ) 转移方程收敛到最优
最优贸易
根据 dp \text{dp} dp y y y d p ( y ) dp(y) d p ( y ) 1 → y 1 \to y 1 → y d p ( y ) dp(y) d p ( y ) y y y π ( y ) \pi (y) π ( y )
d p ( y ) = min ( d p ( y ) , min x ∈ π ( y ) ( d p ( x ) , c o s t ( y ) ) ) dp(y) = \min(dp(y), \min_{x \in \pi(y)}(dp(x), cost(y)))
d p ( y ) = min ( d p ( y ) , x ∈ π ( y ) min ( d p ( x ) , c o s t ( y ) ) )
这样对于任意节点 u u u d p ( u ) dp(u) d p ( u ) 1 → u 1\to u 1 → u 最小花费的城市所需的代价 u → n u \to n u → n 最大花费的城市 即可
思路是类似的,建一张从 n → 1 n \to 1 n → 1 spfa ( n ) \text{spfa}(n) spfa ( n )
d p 2 ( y ) = max ( d p 2 ( y ) , max x ∈ π ( y ) ( d p 2 ( x ) , c o s t ( y ) ) ) dp2(y) = \max(dp2(y), \displaystyle \max_{x \in \pi(y)}(dp2(x), cost(y))) d p 2 ( y ) = max ( d p 2 ( y ) , x ∈ π ( y ) max ( d p 2 ( x ) , c o s t ( y ) ) )
最后枚举每个节点 u u u max ( d p 2 ( u ) − d p ( u ) ) \max (dp2(u) - dp(u)) max ( d p 2 ( u ) − d p ( u ) )
1 2 3 4 add1() 表示添加正向图,add2() 表示反向图 对于单向边 (x, y),执行 add1(x, y), add2(y, x) 如果是双向边 (x, y),还要补上缺少的部分,add1(y, x), add2(x, y)
Dijkstra 和最短路树
Dijkstra \text{Dijkstra} Dijkstra Relax \text{Relax} Relax d ( i ) + w ( i , j ) < d ( j ) d(i) + w(i, j) < d(j) d ( i ) + w ( i , j ) < d ( j ) d ( j ) d(j) d ( j ) p ( j ) = i p(j) = i p ( j ) = i p p p p ( s ) = s p(s) = s p ( s ) = s p ( u ) → u p(u) \to u p ( u ) → u
dijkstra \text{dijkstra} dijkstra vis ( u ) \text{vis}(u) vis ( u ) u u u 这个节点是否被扩展过 spfa \text{spfa} spfa inq ( u ) \text{inq}(u) inq ( u ) u u u 是否在队列中
Warfare and Logistics
对于 G G G ∀ s \forall s ∀ s dijkstra ( s ) \text{dijkstra}(s) dijkstra ( s ) i ∈ V i \in V i ∈ V
δ ( s , i ) = d ( i ) \delta(s, i) = d(i) δ ( s , i ) = d ( i ) s s s C ( s ) = ∑ i = 1 n d ( i ) C(s) = \displaystyle \sum_{i = 1}^{n} d(i) C ( s ) = i = 1 ∑ n d ( i )
本例令 r e s = ∑ s = 1 n C ( s ) res = \displaystyle\sum_{s = 1}^{n} C(s) r e s = s = 1 ∑ n C ( s ) r e s ′ res' r e s ′
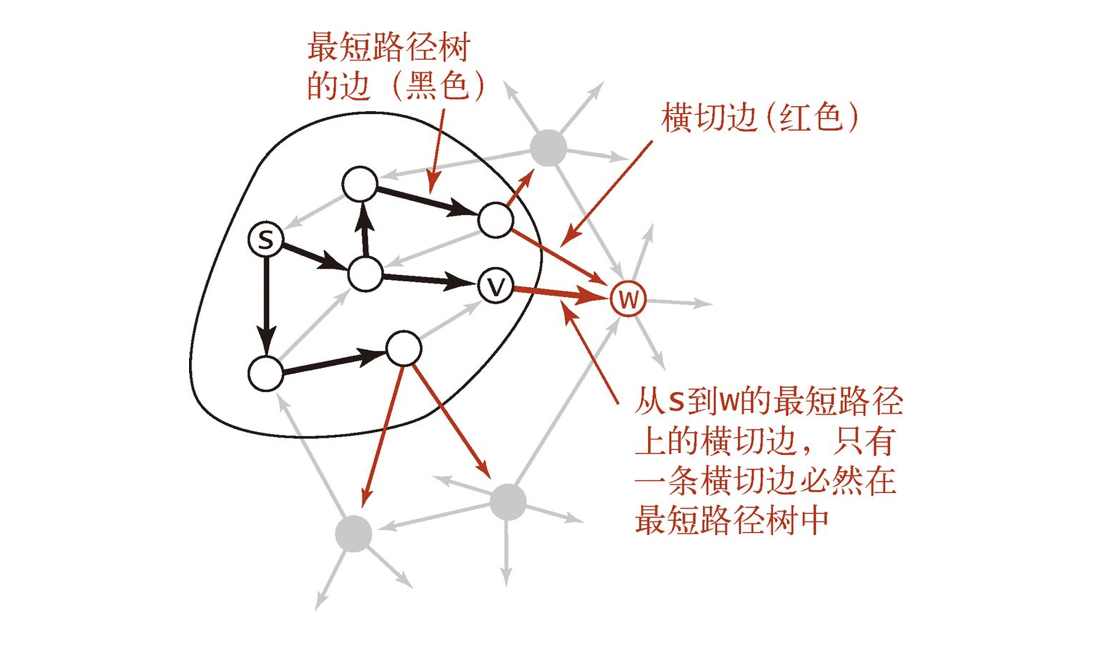
源点为 s s s 前驱子图 V π ( s ) V_{\pi}(s) V π ( s ) s s s e ∉ V π ( s ) e \not\in V_{\pi}(s) e ∈ V π ( s ) V π ( s ) V_{\pi}(s) V π ( s ) n n n n − 1 n-1 n − 1
所以只需要枚举最短路树上的边 ,尝试删除并重新计算最短路,取一个 max \max max
如果删除的边 ∀ e ∉ V π ( s ) \forall e \not\in V_{\pi}(s) ∀ e ∈ V π ( s ) C ( s ) C(s) C ( s )
否则,e ∈ V π ( s ) e \in V_{\pi}(s) e ∈ V π ( s ) dijkstra ( s ) \text{dijkstra}(s) dijkstra ( s ) C [ s ] = ∑ i = 1 n d ( i ) C[s] = \displaystyle \sum_{i = 1}^{n} d(i) C [ s ] = i = 1 ∑ n d ( i )
具体到算法实现上
对每个源点 s ∈ [ 1 , n ] s \in [1, n] s ∈ [ 1 , n ] d ( i ) = + ∞ , p ( i ) = 0 d(i) = +\infty, p(i) = 0 d ( i ) = + ∞ , p ( i ) = 0 dijkstra ( s ) \text{dijkstra}(s) dijkstra ( s ) d ( i ) , p ( i ) d(i), p(i) d ( i ) , p ( i )
C [ s ] + = ∑ i = 1 n d ( i ) C[s] += \displaystyle\sum_{i = 1}^{n} d(i) C [ s ] + = i = 1 ∑ n d ( i )
然后执行 dfs ( s ) \text{dfs}(s) dfs ( s ) { ( u , v ) : p ( v ) = u } \{(u, v): \ p(v) = u\} { ( u , v ) : p ( v ) = u } mark ( s , u , v ) = 1 \text{mark}(s, u, v) = 1 mark ( s , u , v ) = 1
枚举最短路树上的边,其实是枚举每个点对 ( i , j ) (i, j) ( i , j ) ( i , j ) (i, j) ( i , j ) s s s ( i , j ) (i, j) ( i , j ) V π ( s ) V_{\pi}(s) V π ( s ) w ( i , j ) = 0 w(i, j) = 0 w ( i , j ) = 0 dijkstra ( s ) \text{dijkstra}(s) dijkstra ( s ) r e s + = ∑ d ( i ) res += \sum d(i) r e s + = ∑ d ( i ) r e s + = C [ s ] res += C[s] r e s + = C [ s ] r e s res r e s max \max max
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 const int inf = 0x3f3f3f3f; const int maxn = 100 + 10, maxm = 2000 + 10; int n, m, L; vector<int> edges[maxn][maxn]; int ID[maxn][maxn]; typedef pair<int, int> PII; namespace Graph { int idx = 1; int head[maxn], ver[maxm], ne[maxm], e[maxm]; void initG idx = 1; memset(head, 0, sizeof head); memset(ID, 0, sizeof ID); _for(i, 0, maxn) _for(j, 0, maxn) edges[i][j].clear(); } void add(int a, int b, int c) { ver[++idx] = b, e[idx] = c, ne[idx] = head[a], head[a] = idx; ID[a][b] = idx; } int d[maxn], p[maxn], vis[maxn]; void dijkstra(int s) { memset(d, inf, sizeof d); memset(p, 0, sizeof p); memset(vis, 0, sizeof vis); d[s] = 0; priority_queue<PII, vector<PII>, greater<PII> > q; q.push({0, s}); while (q.size()) { auto u = q.top(); q.pop(); int x = u.second; if (vis[x]) continue ; vis[x] = true ; for (int i = head[x]; i; i = ne[i]) { int y = ver[i]; if (e[i] > 0 && d[y] > d[x] + e[i]) { d[y] = d[x] + e[i], p[y] = x; q.push({d[y], y}); } } } } } using namespace Graph; ll C[maxn]; int mark[maxn][maxn][maxn]; void get_mark(int s) { for (int i = 1; i <= n; i++) { if (p[i] == 0) continue ; mark[s][i][p[i]] = mark[s][p[i]][i] = 1; } } void calc memset(C, 0, sizeof C); memset(mark, 0, sizeof mark); for (int s = 1; s <= n; s++) { dijkstra(s); get_mark(s); for (int i = 1; i <= n; i++) C[s] += d[i] == inf ? L : d[i]; } ll sum = 0; for (int s = 1; s <= n; s++) sum += C[s]; printf ("%lld " , sum); } ll del(int i, int j) { ll sum = 0; int id = ID[i][j]; if (edges[i][j].size() == 1) e[id] = e[id^1] = 0; else if (edges[i][j].size() > 1) e[id] = e[id^1] = edges[i][j][1]; for (int s = 1; s <= n; s++) { if (mark[s][i][j] == 0) sum += C[s]; else { dijkstra(s); for (int u = 1; u <= n; u++) sum += d[u] == inf ? L : d[u]; } } e[id] = e[id^1] = edges[i][j][0]; return sum; } int main freopen("input.txt" , "r" , stdin); while (scanf("%d%d%d" , &n, &m, &L) == 3) { initG(); while (m--) { int a, b, c; scanf("%d%d%d" , &a, &b, &c); edges[a][b].push_back(c), edges[b][a].push_back(c); } // add for (int i = 1; i <= n; i++) for (int j = i+1; j <= n; j++) { if (edges[i][j].size() == 0) continue ; sort(edges[i][j].begin(), edges[i][j].end()); add(i, j, edges[i][j][0]), add(j, i, edges[i][j][0]); } // calc calc(); ll res = 0; for (int i = 1; i <= n; i++) for (int j = i+1; j <= n; j++) { if (edges[i][j].size() == 0) continue ; res = max(res, del(i, j)); } printf ("%lld\n" , res); } }
dijkstra 和拓扑排序
SPFA 算法复杂度最坏可能达到 O ( n m ) O(nm) O ( n m ) 道路与航线
对于 dijkstra \text{dijkstra} dijkstra 非负权的连通块中 ,从起点 s s s DAG \text{DAG} DAG
一开始只加入正权边,然后这些边形成正权连通块,将连通块缩点 c c 1 → c c 2 cc_1\to cc_2 c c 1 → c c 2 d ( c c 2 ) = min ( d ( c c 2 ) , d ( c c 1 ) + w ( c c 1 , c c 2 ) ) d(cc_2) = \min (d(cc_2), d(cc_1) + w(cc_1, cc_2)) d ( c c 2 ) = min ( d ( c c 2 ) , d ( c c 1 ) + w ( c c 1 , c c 2 ) ) c c 1 cc_1 c c 1 s s s dijkstra ( s ) \text{dijkstra}(s) dijkstra ( s ) d ( y ) = δ ( s , y ) d(y) = \delta (s, y) d ( y ) = δ ( s , y ) 横跨连通块的边界点,放入拓扑队列中 ,依次进行 dijkstra \text{dijkstra} dijkstra 松弛 ,最后 d d d
具体来说
只加入正权边 ,然后对所有点 ∀ x ∈ G \forall \ x \in G ∀ x ∈ G dfs \text{dfs} dfs [ 1 ⋯ c n t ] [1\cdots cnt] [ 1 ⋯ c n t ] c [ x ] c[x] c [ x ] x x x
加入负权边 ( x , y ) (x, y) ( x , y ) c [ x ] ≠ c [ y ] c[x] \neq c[y] c [ x ] = c [ y ] + + deg ( c [ y ] ) ++\text{deg}(c[y]) + + deg ( c [ y ] )
主算法执行拓扑序 dp,用队列 q q q 连通块拓扑序
找到 deg [ c c ] = 0 \text{deg}[cc] = 0 deg [ c c ] = 0 c c cc c c q [ ⋯ ] ← c c q[\cdots] \leftarrow cc q [ ⋯ ] ← c c d d d d [ ⋯ ] = ∞ , d ( S ) = 0 d[\cdots] = \infty, \ d(S) = 0 d [ ⋯ ] = ∞ , d ( S ) = 0
while q [ ⋯ ] ≠ ∅ : c c ← q . front ( ) \textbf{while} \ q[\cdots] \neq \emptyset: \quad cc \leftarrow q.\text{front}() while q [ ⋯ ] = ∅ : c c ← q . front ( ) ∀ u ∈ V \forall u \in V ∀ u ∈ V c [ u ] = c c c[u] = cc c [ u ] = c c heap \text{heap} heap while heap ≠ ∅ \textbf{while} \ \text{heap} \neq \emptyset while heap = ∅ dijkstra \text{dijkstra} dijkstra 注意这里对每个连通块局部进行 dijkstra \text{dijkstra} dijkstra 每条边 ( x , y ) (x, y) ( x , y ) 只对正权边使用 dijkstra \text{dijkstra} dijkstra 堆只维护 c [ x ] = c [ y ] c[x] = c[y] c [ x ] = c [ y ] ( x , y ) (x, y) ( x , y ) d ( y ) < d ( x ) + e ( x , y ) \quad d(y) < d(x) + e(x, y) d ( y ) < d ( x ) + e ( x , y ) d ( y ) d(y) d ( y ) 仅 c [ x ] = c [ y ] c[x] = c[y] c [ x ] = c [ y ] y y y 检查 ( x , y ) : c [ x ] ≠ c [ y ] and − − deg ( c [ y ] ) = 0 (x, y): \ c[x] \neq c[y] \ \textbf{and} \ --\text{deg}(c[y]) = 0 ( x , y ) : c [ x ] = c [ y ] and − − deg ( c [ y ] ) = 0 q [ ⋯ ] ← c [ y ] q[\cdots] \leftarrow c[y] q [ ⋯ ] ← c [ y ] c [ y ] c[y] c [ y ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 typedef pair<int, int> PII; const int maxn = 25000 + 10, inf = 0x3f3f3f3f; const int maxm = 2e5 + 10; int n, R, P, S; namespace Graph { int idx = 1, cnt = 0; int head[maxn], ver[maxm], e[maxm], ne[maxm], C[maxn], deg[maxn]; void initG idx = 1; cnt = 0; memset(head, 0, sizeof head); memset(C, 0, sizeof C); memset(deg, 0, sizeof deg); } void add(int a, int b, int c) { ver[++idx] = b; e[idx] = c; ne[idx] = head[a]; head[a] = idx; } void dfs(int u) { C[u] = cnt; for (int i = head[u]; i; i = ne[i]) { int v = ver[i]; if (C[v]) continue ; dfs(v); } } void dfs for (int i = 1; i <= n; i++) { if (!C[i]) { ++cnt; dfs(i); } } } } using namespace Graph; int d[maxn], vis[maxn]; void solve memset(d, inf, sizeof d); memset(vis, 0, sizeof vis); d[S] = 0; queue<int> q; for (int i = 1; i <= cnt; i++) if (deg[i] == 0) q.push(i); while (q.size()) { auto cc = q.front(); q.pop(); priority_queue<PII, vector<PII>, greater<PII> > heap; for (int i = 1; i <= n; i++) if (C[i] == cc) heap.push({d[i], i}); while (heap.size()) { int x = heap.top().second; heap.pop(); if (vis[x]) continue ; vis[x] = true ; for (int i = head[x]; i; i = ne[i]) { int y = ver[i]; if (C[y] != C[x] && --deg[C[y]] == 0) q.push(C[y]); if (d[y] > d[x] + e[i]) { d[y] = d[x] + e[i]; if (C[x] == C[y]) heap.push({d[y], y}); } } } } } int main freopen("input.txt" , "r" , stdin); cin >> n >> R >> P >> S; initG(); // add + while (R--) { int a, b, c; scanf("%d%d%d" , &a, &b, &c); add(a, b, c), add(b, a, c); } // dfs dfs(); // add - while (P--) { int a, b, c; scanf("%d%d%d" , &a, &b, &c); add(a, b, c); if (C[a] != C[b]) ++deg[C[b]]; } // solve solve(); for (int i = 1; i <= n; i++) { if (d[i] >= 1e9) puts("NO PATH" ); else printf ("%d\n" , d[i]); } }